Simplifying Radical Expressions
Simplifying radical expressions in algebra is a concept in algebra where we simplify an expression with a radical into a simpler form and remove the radical, if possible. Let us now recall the meaning of radical expressions. Radical expressions are algebraic expressions involving radicals. The radical expressions consist of the root of an algebraic expression (number, variables, or combination of both). The root can be a square root, cube root, or in general, nth root. Simplifying radical expressions implies reducing the algebraic expressions to the simplest form and, if possible, completely eliminating the radicals from the expressions.
In this article, we will learn the steps for simplifying radical expressions with variables and exponents, rules used for simplifying radical expressions with the help of solved examples.
What is Simplifying Radical Expressions?
Simplifying radical expressions is a process of reducing the radical expressions to the simplest form and removing the radical completely, if possible. If a radical expression is present in the denominator of an algebraic expression, we multiply the numerator and denominator with the appropriate radical expression (for example, conjugate in case of a binomial, and the same radical in case of a monomial) for simplifying the radical expression.
Let us consider an example for simplifying radical expressions. Consider f(x) = √(4x2y6). To simplify f(x), we need to look for pairs of identical factors of 4x2y6. f(x) = √(2 × 2 × x × x × y3 × y3) = √(22 × x2 × (y3 × y3)) = 2 |x| |y3| (Because √x2 is always non-negative, that is, |x|). Below is the image of an example of radical expression and its components.
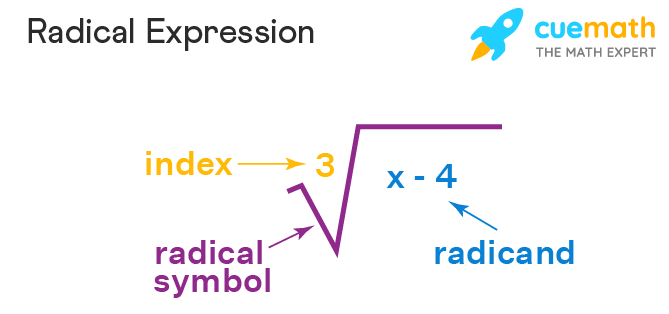
Steps for Simplifying Radical Expressions
Simplifying radical expressions is a process of eliminating radicals or reducing the expressions consisting of square roots, cube roots, or in general, nth root to simplest form. Let us consider a few examples for simplifying radical expressions step-wise. We will recall some tricks that we use for simplifying radical expressions such as multiplying and dividing with the conjugate, finding factors in pairs for a square root, etc.
Simplifying Radical Expressions with Square Root
For simplifying radical expressions with square root, let us consider an example. Consider the radical expression √486. We will simplify this radical expression into the simplest form until no further simplification can be done.
- Step 1: Find the factors of the number under the radical.
486 = 3 × 3 × 3 × 3 × 3 × 2 - Step 2: Write the number under the radical as a product of its factors as powers of 2.
486 = 32 × 32 × 3 × 2 - Step 3: Write the factors outside the radical which have the power 2.
√486 = √(32 × 32 × 3 × 2) = 3 × 3 √(3 × 2) = 9√(3 × 2) - Step 4: Simplify the radical until no further simplification can be done
√486 = 9√(3 × 2) = 9√6. No further multiplication can be done now.
Hence, we have simplified the radical expression √486 as 9√6 and it cannot be simplified more.
Simplifying Radical Expressions with Cube Root or Higher Root
For simplifying radical expressions with cube root or higher roots, let us consider an example. Consider the radical expression \(\sqrt[5]{2^6\times 2\times 3^5\times 11}\). We will simplify this radical expression into the simplest form until no further simplification can be done.
- Step 1: Determine the prime factors of the number under the root.
The prime factors of 26 × 2 × 35 × 11 are 2, 3, 11 - Step 2: Write the prime factors in groups.
\(\sqrt[5]{2^6\times 2\times 3^5\times 11} = \sqrt[5]{2^7\times 3^5\times 11}\) - Step 3: Simplify any multiplication and exponents.
\( \sqrt[5]{2^7\times 3^5\times 11} = \sqrt[5]{2^5\times 2^2 \times 3^5\times 11} = 2\times 3 \sqrt[5]{2^2\times 11}\) - Step 4: Simplify the radical until no further simplification can be done.
\( \sqrt[5]{2^7\times 3^5\times 11} = 2\times 3 \sqrt[5]{2^2\times 11} = 6\sqrt[5]{4\times 11} = 6\sqrt[5]{44}\)
Simplifying Radical Expressions with Variables
The process of simplifying radical expressions with variables is similar to that of numbers. We factorize the variables along with the numbers. Let us consider an example of simplifying radical expressions with variables for a better understanding. Consider the radical expression √(100x4y6z3).
- Step 1: Write the number under the radical as a product of its prime factors and expand the variables.
√100x4y6z3 = √(2 × 2 × 5 × 5 × x × x × x × x × y × y × y × y × y × y × z × z × z) - Step 2: Combine the factors in pairs of identical factors.
√(2 × 2 × 5 × 5 × x × x × x × x × y × y × y × y × y × y × z × z × z) = √(22 × 52 × x2 × x2 × y2 × y2 × y2 × z2 × z) = √(22 × 52 × (x2)2 × (y3)2 × z2 × z) - Step 3: Bring out the factors with powers 2 out of the radical. Please note that √x2 is always non-negative. So, use the absolute value symbol to make the value non-negative.
√100x4y6z3 = √(22 × 52 × (x2)2 × (y3)2 × z2 × z) = 2 × 5 × x2 × |y3| × |z| × √z - Step 4: Simplify the radical until no further simplification can be one
√100x4y6z3 = 10 x2 |y3| |z| √z
Rules for Simplifying Radical Expressions
Now that we have learned how to simplify different kinds of radical expressions. Let us go through some rules for simplifying radical expressions which can be used to simplify complex radical expressions. If a, b are real numbers, then we have:
- √ab = √a√b
- √(a/b) = √a/√b, b ≠ 0
- √a + √b ≠ √(a + b)
- √a - √b ≠ √(a - b)
Tips and Tricks for Simplifying Radical Expressions
- For simplifying radical expression with a radical in the denominator, multiply the numerator and the denominator with the conjugate of the denominator. For example, simplify radical expression (√2 + √3)/(√5 - √2). We will multiply the numerator and denominator of this expression with the conjugate of √5 - √2 which is √5 + √2 and use the algebraic identity a2 - b2 = (a - b)(a + b).
(√2 + √3)/(√5 - √2) = (√2 + √3) × (√5 + √2)/(√5 - √2) × (√5 + √2)
= (√2√5 + √3√5 + √2√2 + √3√2)/((√5)2 - (√2)2)
= (√10 + √15 + 2 + √6)/(5 - 2)
= (√10 + √15 + 2 + √6)/3
Hence, we have simplified the radical expression with radicals in the denominator and no further simplification can be done. - Since the square of a negative number is the same as the square of the positive number with the same magnitude, therefore we need to remember that the square root of a number will always be non-negative. Hence we take the absolute value.
Topics Related to Simplifying Radical Expressions
Simplifying Radical Expressions Examples
-
Example 1: Simplify √12/√5 using the rules for simplifying radical expressions.
Solution: To simplify the radical expression √12/√5, we need to eliminate the radicals from the denominator. We will multiply the numerator and denominator with √5.
√12/√5 = (√12 × √5)/(√5 × √5)
= √(12 × 5)/√(5 × 5)
= √60/√25
= √(4 × 15)/5
= (2√15)/5
= (2/5)√15
Answer: √12/√5 = (2/5)√15
-
Example 2: Simplify radical expression (10b2c2)/(c√(4b3))
Solution: (10b2c2)/(c√(4b3)) = (10b2c2)/2c√(b2b)
= (10b2c2)/2bc√b
= 5bc/√b
= (5bc × √b)/(√b × √b)
= (5bc√b)/b
= 5c√b
Answer: (10b2c2)/(c√(4b3)) = 5c√b

FAQs on Simplifying Radical Expressions
What is Simplifying Radical Expressions in Algebra?
Simplifying radical expressions is a process of reducing the radical expressions to the simplest form and removing the radical completely, if possible.
When Do You Use Absolute Value When Simplifying Radical Expressions?
The even power of any number is always positive, therefore any even-numbered root must be a positive number (otherwise it is imaginary), and hence the absolute value must be used when simplifying radical expressions with variables, which ensures the answer is positive. When working with radical expressions with odd radicals, this requirement does not apply because odd roots exist for negative numbers.
How to Do Simplifying Radical Expressions?
Simplifying radical expressions is a process of eliminating radicals or reducing the expressions consisting of square roots, cube roots, or in general, nth root to simplest form.
What Mathematical Concepts are Important in Simplifying Radical Expressions?
All mathematical concepts including addition, subtraction, multiplication, and division are important in simplifying radical expressions along with the order of operations.
What are Some Important Rules for Simplifying Radical Expressions?
Some rules to keep in mind while simplifying radical expressions for real numbers a, b are:
- √ab = √a√b
- √(a/b) = √a/√b, b ≠ 0
- √a + √b ≠ √(a + b)
- √a - √b ≠ √(a - b)
What is the Point of Simplifying Radical Expressions?
Simplifying radical expressions expression is important before addition or subtraction of expressions to identify like terms that can be added or subtracted, and hence reach the solution.
visual curriculum