System of Equations
In mathematics, a system of equations, also known as a set of simultaneous equations or an equation system, is a finite set of equations for which we sought common solutions. In systems of equations, variables are related in a specific way in each equation. i.e., the equations can be solved simultaneously to find a set of values of variables that satisfies each equation.
System of linear equations finds applications in our day-to-day lives in modelling problems where the unknown values can be represented in form of variables. Solving system of equations involves different methods such as substitution, elimination, graphing, etc. Let us look into each method in detail.
What is a System of Equations?
In algebra, a system of equations comprises two or more equations and seeks common solutions to the equations. "A system of linear equations is a set of equations which are satisfied by the same set of values of variables."
System of Equations Example
A system of equations as discussed above is a set of equations that seek a common solution for the variables included. The following set of linear equations is an example of the system of equations:
- 2x - y = 12
- x - 2y = 48
Note that the values x = -8 and y = -28 satisfy each of these equations and hence the pair (x, y) = (-8, -28) is the solution of the above system of equations. But how to solve system of equations? Let us see.
Solutions of System of Equations
Solution of system of equations is the set of values of variables that satisfies each linear equation in the system. The main reason behind solving an equation system is to find the value of the variable that satisfies the condition of all the given equations true. There systems of equations are classified into 3 types depending on their number of solutions:
- Linear System with "Unique solution"
- Linear System with "No solution"
- Linear System with "Infinitely many solutions"
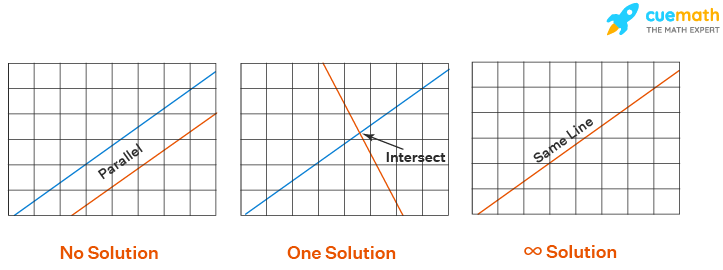
We know that every linear equation represents a line on the coordinate plane. In this perception, the above figure should give more sense to understanding the different types of solutions of system of equations.
Unique Solution of a System of Equations
A system of equations has unique solution when there is only set of variables exist that satisfy each equation in the system. In terms of graphs, a system with a unique solution has lines (representing the equations) that intersect (at one point).
No Solution
A system of equations has no solution when there exists no set of variables that satisfy each linear equation in the system. If we graph that kind of system, the resulting lines will be parallel to each other.
Infinite Many Solutions
A system of equations can have infinitely many solutions when there exist infinite sets of variables that satisfy each equation. In such cases, the lines corresponding to the linear equations would overlap each other on the graph. i.e., both equations represent the same line. Since a line has infinite points on it, each point on it becomes a solution of the system.
Solving System of Equations
Solving a system of equations means finding the values of the variables used in the set of equations. Any system of equations can be solved in different methods.
- Substitution Method
- Elimination Method
- Graphical Method
- Cross-multiplication method
To solve a system of equations in 2 variables, we need at least 2 equations. Similarly, for solving a system of equations in 3 variables, we will require at least 3 equations. Let us understand 3 ways to solve a system of equations given the equations are linear equations in two variables.
☛ Also Check: Solving System of Linear Equations
Solving System of Linear Equations By Substitution Method
For solving the system of equations using the substitution method given two linear equations in x and y, in one of the equations, express y in terms x in one of the equations and then substitute it in the other equation.
Example: Solve the system of equations using the substitution method.
3x − y = 23 → (1)
4x + 3y = 48 → (2)
From (1), we get:
y = 3x − 23 → 3
Plug in y in (2),
4x + 3 (3x − 23) = 48
13x − 69 = 48
13x = 117
⇒x = 9
Now, plug in x = 9 in (1)
y = 3 × 9 − 23 = 4
Hence, x = 9 and y = 4 is the solution of the given system of equations.
Solving System of Equations By Elimination Method
Using the elimination method to solve the system of equations, we eliminate one of the unknowns, by multiplying equations by suitable numbers, so that the coefficients of one of the variables become the same.
Example: Solve the following system of linear equations by elimination method.
2x + 3y = 4 → (1) and 3x + 2y = 11 → (2)
The coefficients of y are 3 and 2; LCM (3, 2) = 6
Multiplying Equation (1) by 2 and Equation (2) by 3, we get
4x + 6y = 8 → (3)
9x + 6y = 33 → (4)
On subtracting (3) from (4), we get
5x = 25
⇒x = 5
Plugging in x = 5 in (2) we get
15 + 2y = 11
⇒y = −2
Hence, x = 5, y = −2 is the solution.
Solving System of Equations by Graphing
In this method, solving system of linear equations is done by plotting their graphs. "The point of intersection of the two lines is the solution of the system of equations using graphical method."
Example: 3x + 4y = 11 and -x + 2y = 3
Find at least two values of x and y satisfying equation 3x + 4y = 11
| x | 1 | 3 |
|---|---|---|
| y | 2 | 0.5 |
So we have 2 points A (1, 2) and B (3, 0.5).
Similarly, find at least two values of x and y satisfying the equation -x + 2y = 3
| x | -3 | 3 |
|---|---|---|
| y | 0 | 3 |
We have two points C(-3, 0) and D( 3, 3).
Plotting these points on the graph we can get the lines in a coordinate plane as shown below.

We observe that the two lines intersect at (1, 2). So, x = 1, y = 2 is the solution of given system of equations. Methods I and II are the algebraic way of solving simultaneous equations and III is the graphical method.
Solving System of Equations Using Cross-multiplication method
In this method, we solve the systems of equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 using the cross-multiplication formula:
x / (b1c2 - b2c1) = -y / (a1c2 - a2c1) = 1 / (a1b2 - a2b1)
For more detailed information of this method, click here.
Solving System of Equations Using Matrices
The solution of a system of equations can be solved using matrices. In order to solve a system of equations using matrices, express the given equations in standard form, with the variables and constants on respective sides. for the given equations,
a\(_1\)x + \(b_1\)y + \(c_1\)z = \(d_1\)
a\(_2\)x + \(b_2\)y + \(c_2\)z = \(d_2\)
a\(_3\)x + \(b_3\)y + \(c_3\)z = \(d_3\)
we can express them in the form of matrices as,
\(\left[\begin{array}{ccc}
a_1x + b_1y + c_1 z \\
a_2x + b_2y + c_2 z \\
a_3x + b_3y + c_3 z
\end{array}\right] = \left[\begin{array}{ccc}
d_1 \\
d_2 \\
d_3
\end{array}\right]\)
⇒\(\left[\begin{array}{ccc}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2 \\
a_3 & b_3 & c_3
\end{array}\right] + \left[\begin{array}{ccc}
x \\
y \\
z
\end{array}\right] = \left[\begin{array}{ccc}
d_1 \\
d_2 \\
d_3
\end{array}\right]\)
⇒ AX = B
Here,
A = \(\left[\begin{array}{ccc}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2 \\
a_3 & b_3 & c_3
\end{array}\right]\), X = \(\left[\begin{array}{ccc}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
d_1 \\
d_2 \\
d_3
\end{array}\right]\)
⇒ The solution of the system is given by the formula X = A-1B, where A-1 = inverse of the matrix A. To understand this method more in detail, click here.
Alternatively, Cramer's rule can also be used to solve the system of equations using determinants.
Applications of System of Equations
Systems of equations are a very useful tool and find application in our day-to-day lives for modeling real-life situations and analyzing questions about them.
☛Check:
For applying the concept of the system of equations, we need to translate the given situation into two linear equations in two variables, then further solve to find the solution of linear programming problems. Any method to solve the system of equations, substitution, elimination, graphical, etc methods. Follow the below-given steps to apply the system of equations to solve problems in our daily lives,
- To translate and represent the given situation in form of a system of equations, identify unknown quantities in a problem and represent them with variables.
- Write a system of equations modelling the conditions of the problem.
- Solve the system of equations.
- Check and express the obtained solution in terms of the given context.
☛Related Articles:
Check these articles related to the concept of the system of equations.
System of Equations Examples
-
Example 1: In a ΔLMN, ∠N = 3∠M = 2(∠L+∠M). Calculate the angles of ΔLMN using this information.
Solution:
Let ∠L = x° and ∠M = y°.
Then,
∠N = 3∠M = (3y)°.
Now,
∠L + ∠M + ∠N = 180°
∴ x + y + 3y = 180
x + 4y = 180 ... (1)
From the given equation, 3∠M = 2(∠L+∠M)
∴ 3y = 2(x + y) ⇒ 2x - y = 0 ... (2)
On multiplying (2) by 4 and adding the result to (1), we get
9x = 180
x = 20
Substitute this in (2):
40 - y = 0 ⇒ y = 40
Therefore, ∠L = 20° and ∠M = 40°.
Therefore, the third angle is, ∠N = 180 - (20 + 40) = 120°.
Answer: ∠L = 20°, ∠M = 40°, and ∠N = 120°. -
Example 2: Peter is three times as old as his son. 5 years later, he shall be two and half times as old as his son. What's Peter's present age?
Solution:
Let Peter's age be x years and his son's age be y years. Then by given info,
x = 3y ... (1)
5 years later,
Peter's age = x + 5 years and his son's age = y + 5 years.
By the given condition,
x + 5 = 5/2 (y + 5)
2x - 5y - 15 = 0 ... (2)
From (1), we have x = 3y. Substitute this in (2):
2(3y) - 5y - 15 = 0
y = 15
Substitute this in (1): x = 3(15) = 45
Thus, the solution of the given system is (x, y) = (45, 15).
Answer: Present age of Peter = 45 years; Present age of son = 15 years.
-
Example 3: Tressa starts her job with a certain monthly salary and earns a fixed increment every year. If her salary was $1500 after 4 years and $1800 after 10 years of service, find her starting salary and annual increment.
Solution:
Let her starting salary be x and annual increment be y.
After 4 years, her salary was $1500
x + 4y = 1500 ... (1)
After 10 years, her salary was $1800
x + 10y = 1800 ... (2)
Subtracting Eqn (1) from (2), we get
6y = 300
∴ y = 50
On putting y = 50 in (1), we get x = 1300.
Answer: Starting salary was $1300 and annual increment is $50.

FAQs on System of Equations
What is a System of Equations in Mathematics?
A system of equations in mathematics is a set of linear equations that need to be solved to find a common solution. A real-life problem with two or more unknowns can be converted into a system of equations and can be solved to find a set of values of variables that satisfy all equations.
How Do You Solve a System of Equations?
Solving a system of equations is computing the unknown variables still balancing the equations on both sides. We solve an equation system to find the values of the variables that satisfy the condition of all the given equations. There are different methods to solve a system of equations,
- Graphical method
- Substitution method
- Elimination method
- Cross-multiplication method
How Do You Create a System of Equations with Two Variables?
To create a system of equations with two variables:
- First, identify the two unknown quantities in the given problem.
- Next, find out the two conditions given and frame equations for each of them.
How to Solve a System of Equations by Substitution Method?
The substitution method is one of the ways to solve a system of equations in two variables, given the set of linear equations. In this method, we substitute the value of a variable found by one equation in the second equation.
How to Solve a System of Equations Using the Elimination Method?
The elimination method is used to solve a system of linear equations. In the elimination method, we eliminate one of the two variables by multiplying each equation with the required numbers and try to solve equations with another variable. In this process, finding LCM of coefficients would be helpful.
What is the Purpose of Graphing Systems of Equations?
To solve the system of equations, given a set of linear equations graphically, we need to find at least two solutions for the respective equations. We observe the pattern of lines after plotting the points to infer it is consistent, dependent, or inconsistent.
- If the two lines are intersecting at the same point, then the intersection point gives a unique solution for the system of equations.
- If the two lines coincide, then in this case there are infinitely many solutions.
- If the two lines are parallel, then in this case there is no solution.
What are Homogeneous System of Linear Equations?
The homogeneous system of linear equations is a set of linear equation each one of which has its constant term to be 0. The process of solving these kind of systems can be learnt in detailed by clicking here.
How to Solve a System of Equations With Cross Multiplication Method?
While solving a system of equations using the cross-multiplication method, we use the formula x / (b1c2 - b2c1) = -y / (a1c2 - a2c1) = 1 / (a1b2 - a2b1) to solve the system a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0.
How do you Solve a System of Equations Using 2 Equations with 3 Variables?
An equation with 3 variables represents a plane.
- Step 1) To solve a system of 2 equations with 3 variables say x, y, and z, we will consider the 1st two equations and eliminate one of the variables, say x, to obtain a new equation.
- Step 2) Next, we write the 2nd variable, y in terms of z from the new equation and substitute it in the third equation.
- Step 3) Assuming z = a, we will obtain values of x and y also in terms of 'a'.
- Step 4) Once, we know the value of a, we can find the values of x and y in terms of 'a'.
What is the Solution to the System of Equations and How to Find It?
Solving system of equations is finding the values of variables that satisfy each equation in that system. There are three main methods to solving system of equations, they are:
- Substitution Method
- Cross-multiplication method
- Elimination Method
- Graphical Method
Where Can I Find System of Linear Equations Calculator?
The system of linear equations calculator is available here. This allows us to enter the linear equations. Then it will show the solution along with step-by-step solution.
visual curriculum