Axis of Symmetry
The axis of symmetry is an imaginary straight line that divides a shape into two identical parts, thereby creating one part as the mirror image of the other part. When folded along the axis of the symmetry, the two parts get superimposed. The straight line is called the line of symmetry/the mirror line. This line can be vertical, horizontal, or slanting.
We can see this axis of symmetry even in nature such as flowers, riverbanks, buildings, leaves, and so on. We can observe this in the Taj Mahal, the iconic marble structure in India.
What is Axis of Symmetry?
The axis of symmetry is a straight line that makes the shape of the object symmetrical. The axis of symmetry creates the exact reflections on each of its sides. It can be either horizontal, vertical, or lateral. If we fold and unfold an object along the axis of symmetry, the two sides are identical. Different shapes have different lines of symmetry. A square has four lines of symmetry, a rectangle has 2 lines of symmetry, a circle has infinite lines of symmetry and a parallelogram has no line of symmetry. A regular polygon of 'n' sides has 'n' axes of symmetry.

Axis of Symmetry Definition
The axis of symmetry is an imaginary line that divides a figure into two identical parts such that each part is a mirror reflection of one another. When the figure is folded along the axis of symmetry, the two identical parts superimpose.
Axis of Symmetry of a Parabola
A parabola has one line of symmetry. The axis of the symmetry is the straight line that divides a parabola into two symmetrical parts. The parabola can be in four forms. It can be either horizontal or vertical, facing left or right. The axis of symmetry determines the form of the parabola.
- If the axis of symmetry is vertical, then the parabola is vertical (opens up/down).
- If it is horizontal, then the parabola is horizontal (opens left/right).

The axis of symmetry which is horizontal has zero slope, and the axis of symmetry which is vertical has an undefined slope.
Axis of Symmetry Equation
The vertex is the point where the axis of symmetry intersects the parabola. This is the key point to determine its equation. If the parabola opens up or down, the axis of symmetry is vertical and in this case, its equation is the vertical line that passes through its vertex. If the parabola opens right or left, the axis of symmetry is horizontal and its equation is the horizontal line that passes through its vertex. i.e.,
- The axis of symmetry equation of a parabola whose vertex is (h, k) and opens up/down is x = h.
- The axis of symmetry equation of a parabola whose vertex is (h, k) and opens left/right is y = k.
Axis of Symmetry Formula
The axis of symmetry formula is applied on quadratic equations where the standard form of the equation and the line of symmetry are used. A line that divides or bifurcates any object into two equal halves, both halves of which are mirror images of each other is called the axis of symmetry. This line of axis dividing the objects could be any one of the three types that are: horizontal (x-axis), vertical (y-axis), or inclined line.
The equation of the axis of symmetry can be represented when a parabola is in two forms:
- Standard form
- Vertex form
Standard form
The quadratic equation in standard form is, y = ax2+ b x+c
where a, b, and c are real numbers.
Here, the axis of symmetry formula is: x = - b/2a.
Vertex form
The quadratic equation in vertex form is, y = a (x-h)2 + k
where (h, k) is the vertex of the parabola.
Here, the axis of symmetry formula is x = h.
Derivation of the Axis of Symmetry for Parabola
The axis of symmetry always passes through the vertex of the parabola. Thus identification of the vertex helps us to calculate the position of the axis of symmetry. Axis of symmetry formula for a parabola is, x = -b/2a. Let us derive the equation of the axis of symmetry.
The quadratic equation of a parabola is, y = ax2 + bx + c (up/down parabola).
The constant term 'c' does not affect the parabola.Therefore, let us consider, y = ax2 + bx.
The axis of symmetry is the midpoint of its two x-intercepts. To find the x-intercept, substitute y = 0.
x(ax+b)=0
x = 0 and (ax+b)=0
x = 0 and x = -b/a
The mid-point formula is x = (x1 + x2) / 2
x= [0 + (-b/a)] / 2
Therefore x = -b/2a
Note: If the parabola is left/right open, then find the midpoint of y-intercepts.
Find Axis of Symmetry
Example 1: Find the axis of symmetry of the quadratic equation y = x2 - 4x + 3.
Solution:
Given: y = x2 - 4x + 3
Using axis of symmetry formula,
x = -b/2a
x = -(-4)/2(1)
x = 4/2
= 2
Therefore, axis of symmetry of equation y = x2 - 4x + 3 is x = 2.
Example 2: Find the axis of symmetry of a parabola y = 4x2.
Solution:
Using axis of symmetry formula,
x = -b/2a
x = -(0)/2(4)
x = 0
Therefore, axis of symmetry of parabola y = 4x2 is x = 0.
Identification of the Axis of Symmetry
Let us identify the axis of symmetry for the given parabola using the formula learned in the previous section.
1) Consider equation y = x2- 3x + 4. Comparing this with the equation of the standard form of the parabola (y = ax2 + bx + c), we have
a = 1, b = -3 and c = 4
This is a vertical parabola. Thus it has a vertical axis of symmetry.
We know that x = -b/2a is the equation of the axis of symmetry.
x = -(-3)/2(1) = 1.5
x = 1.5 is the axis of symmetry of the parabola y = x2- 3x + 4.
2) Let us consider another example. x = 4y2+5y+3.
Comparing with the standard form of the quadratic equation, we get a = 4, b = 5, and c = 3. This parabola is horizontal and the axis of symmetry is horizontal too.
We know that y = -b/2a is the equation of the axis of symmetry.
y = -b/2a
y = -5/2(4)
y = -0.625
3) If two points are at the same distance from the vertex of the parabola are given, then we determine the equation of the axis of symmetry by finding the midpoint of those points. Suppose the two points (3, 4) and (9, 4) are points on a parabola, then the vertex passes through the intercept which forms the midpoint of these given points. Thus x = (3+9)/2 = 12/2 = 6. Therefore, the equation of the axis of symmetry is x = 6.
Example: If the axis of symmetry of the equation y = qx2 – 32x – 10 is 8, then find the value of q.
Solution: Given,
y = qx2 – 32x – 10
Axis of symmetry is x = 8
Using the formula:
x = -b/2a
where a = q, b = -32 and x = 8
8 = -(-32) / (2 × q)
8 = 32/2q
16q = 32
q = 2
Therefore, the value of q = 2.
Important Notes on Axis of Symmetry
- An axis of symmetry is an imaginary line that divides a figure into two identical parts that are mirror images of one another.
- For parabola y = ax2+ b x+c, the axis of symmetry is given by x = -b/2a
- A regular polygon of 'n' sides has 'n' axes of symmetry.
☛ Related Articles:
Axis of Symmetry Examples
-
Example 1: Find the equation of the axis of symmetry of the given parabola.
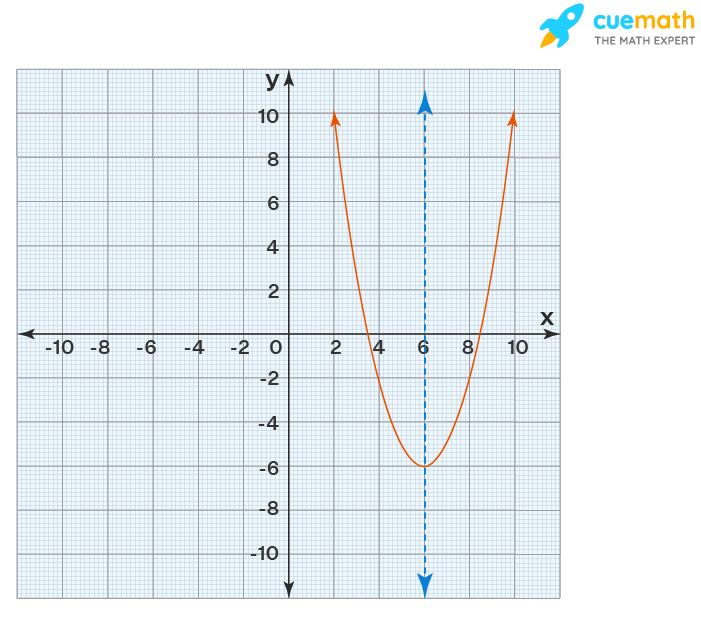
Solution:
Here the vertex = (6, -6)
The axis of symmetry intersects the parabola at its vertex and it is a vertical line since the parabola opens up.
Hence its equation is:
x = 6
Answer: x = 6.
-
Example 2: Which line divides the parabola 3x2-12 x + 5 = 0 into two equal parts? Graph it.
Solution:
Comparing with the standard form of the quadratic equation ax2 + bx + c, we have a = 3, b = -12 & c = 5
We know that, x = -b/2a is the equation of axis of symmetry.
x = -(-12)/2(3)
x = 2
Let us graph it now.
Answer: x = 2 is drawn.
-
Example 3: Find the equation of the line that divides the given parabola into two equal parts.

Solution:
Here the vertex = (-4,0).
The axis of symmetry intersects the parabola at its vertex and is a horizontal line in this case as the parabola opens sideways.
Hence, its equation is y = 0
Answer: y = 0.

FAQs on Axis of Symmetry
What is Axis of Symmetry in Algebra?
The axis of symmetry is an imaginary line that divides a figure into two identical parts such that each part is a mirror reflection of one another. A regular polygon of 'n' sides has 'n' axes of symmetry.
What is The Axis of Symmetry Definition?
The axis of symmetry is an imaginary straight line that divides the shape into two identical parts or that makes the shape symmetrical. For example, a square has 4 and a rectangle has 2 axes of symmetry.
What is the Axis of Symmetry Formula?
The axis of symmetry formula uses the standard form of the quadratic equation as well as the vertex form. The symmetry cuts any geometric shape into two equal halves. The axis of symmetry formula is given as, for a quadratic equation with standard form as y = ax2 + bx + c, is: x = -b/2a. If the parabola is in vertex form y = a(x-h)2 + k, then the formula is x = h.
What is the Formula to Calculate the Axis of Symmetry for Standard Form?
The formula used to find the axis of symmetry for a quadratic equation with standard form as y = ax2 + bx + c, is: x = -b/2a.
What is the Axis of Symmetry Formula for Vertex Form?
The quadratic equation is represented in the vertex form as: y = a(x−h)2 + k , where (h, k) is the vertex of the parabola. Since the axis of symmetry and the vertex form lie on the same line, the formula is x = h.
Find the Axis of Symmetry of the Quadratic Equation y = 5x2 - 10x + 3.
Given: y = 5x2 - 10x + 3
Using axis of symmetry formula,
x = -b/2a
x = -(-10)/2(5)
x = 10/10
x = 1
Therefore, axis of symmetry of equation y = 5x2 - 10x + 3 is x = 1.
What is Axis of Symmetry of a Parabola?
The axis of the symmetry is the straight line that divides a parabola into two symmetrical parts. It passes through the vertex of the parabola. The axis of symmetry of a parabola can be horizontal or vertical.
How Do You Find The Axis of Symmetry Using The Vertex Form of Equation?
The quadratic equation in the vertex form is y = a(x-h)2+k. The axis of symmetry is where the vertex intersects the parabola at the point denoted by the vertex (h, k). h is the x coordinate. and in the vertex form, x = h and h =-b/2a where b and a are the coefficients in the standard form of the equation, y = ax2 + bx + c.
What is the Axis of Symmetry on a Graph?
The horizontal or the vertical line on the graph that passes through the vertex of the parabola forms the axis of symmetry of a parabola. In the case of any other graph, the axis of symmetry is the equation of a line that divides the figure into two equal parts where one is the mirror image of the other.
Is the Axis of Symmetry the Same as the Line of Symmetry?
Yes, the line of symmetry and the axis of symmetry are the same. They are imaginary lines that divide a figure into two identical parts and each part is a mirror reflection of one another. When the figure is folded along this line, the two parts superimpose.
visual curriculum