Continuous Random Variable
Continuous random variable is a random variable that can take on a continuum of values. In other words, a random variable is said to be continuous if it assumes a value that falls between a particular interval.
Continuous random variables are used to denote measurements such as height, weight, time, etc. The area under a density curve is used to represent a continuous random variable. In this article, we will learn about the definition of a continuous random variable, its mean, variance, types, and associated examples.
What is a Continuous Random Variable?
A continuous random variable and a discrete random variable are the two types of random variables. A random variable is a variable whose value depends on all the possible outcomes of an experiment. A continuous random variable is defined over a range of values while a discrete random variable is defined at an exact value.
Continuous Random Variable Definition
A continuous random variable can be defined as a random variable that can take on an infinite number of possible values. Due to this, the probability that a continuous random variable will take on an exact value is 0. The cumulative distribution function and the probability density function are used to describe the characteristics of a continuous random variable.
Continuous Random Variable Example
Suppose the probability density function of a continuous random variable, X, is given by 4x3, where x ∈ [0, 1]. The probability that X takes on a value between 1/2 and 1 needs to be determined. This can be done by integrating 4x3 between 1/2 and 1. Thus, the required probability is 15/16.
Continuous Random Variable Formulas
The probability density function (pdf) and the cumulative distribution function (CDF) are used to describe the probabilities associated with a continuous random variable. The continuous random variable formulas for these functions are given below.
PDF of Continuous Random Variable
The probability density function of a continuous random variable can be defined as a function that gives the probability that the value of the random variable will fall between a range of values. Let X be the continuous random variable, then the formula for the pdf, f(x), is given as follows:
f(x) = \(\frac{\mathrm{d} F(x)}{\mathrm{d} x}\) = F'(x)
where, F(x) is the cumulative distribution function.
For the pdf of a continuous random variable to be valid, it must satisfy the following conditions:
- \(\int_{-\infty }^{\infty }f(x)dx = 1\). This means that the total area under the graph of the pdf must be equal to 1.
- f(x) > 0. This implies that the probability density function of a continuous random variable cannot be negative.
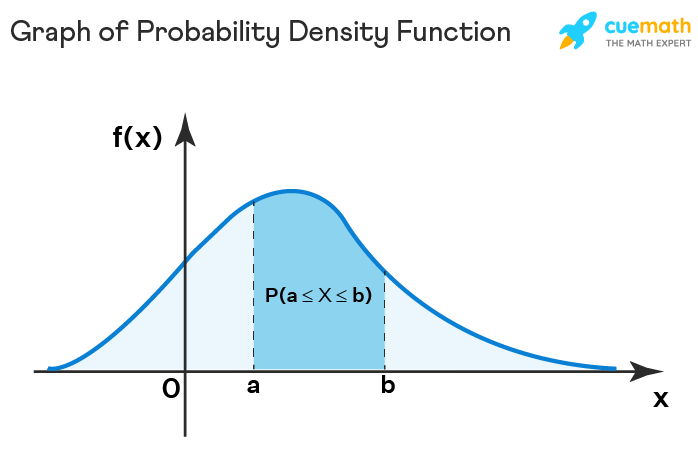
CDF of Continuous Random Variable
The cumulative distribution function of a continuous random variable can be determined by integrating the probability density function. It can be defined as the probability that the random variable, X, will take on a value that is lesser than or equal to a particular value, x. The formula for the cdf of a continuous random variable, evaluated between two points a and b, is given below:
P(a < X ≤ b) = F(b) - F(a) = \(\int_{a}^{b}f(x)dx\)
Mean and Variance of Continuous Random Variable
The mean and variance of a continuous random variable can be determined with the help of the probability density function, f(x).
Mean of Continuous Random Variable
The mean of a continuous random variable can be defined as the weighted average value of the random variable, X. It is also known as the expectation of the continuous random variable. The formula is given as follows:
E[X] = \(\mu = \int_{-\infty }^{\infty}xf(x)dx\)
Variance of Continuous Random Variable
The variance of a continuous random variable can be defined as the expectation of the squared differences from the mean. It helps to determine the dispersion in the distribution of the continuous random variable with respect to the mean. The formula is given as follows:
Var(X) = \(\sigma ^{2} = \int_{-\infty }^{\infty }(x - \mu )^{2}f(x)dx\)
Continuous Random Variable Types
A continuous random variable is usually used to model situations that involve measurements. For example, the possible values of the temperature on any given day. As the temperature could be any real number in a given interval thus, a continuous random variable is required to describe it. Some important continuous random variables associated with certain probability distributions are given below.
Uniform Random Variable
A continuous random variable that is used to describe a uniform distribution is known as a uniform random variable. Such a distribution describes events that are equally likely to occur. The pdf of a uniform random variable is as follows:
\(f(x) = \left\{\begin{matrix} \frac{1}{b-a} & a\leq x\leq b\\ 0 & otherwise \end{matrix}\right.\)
Normal Random Variable
A continuous random variable that is used to model a normal distribution is known as a normal random variable. If the parameters of a normal distribution are given as \(X \sim N(\mu ,\sigma ^{2})\) then the formula for the pdf is given as follows:
f(x) = \(\frac{1}{\sigma \sqrt{2\Pi}}e^{\frac{-1}{2}\left ( \frac{x - \mu }{\sigma } \right )^{2}}\)
where,
\(\mu\) = mean
\(\sigma\) = standard deviation
\(\sigma\)2 = variance.
A normal distribution where \(\mu\) = 0 and \(\sigma\)2 = 1 is known as a standard normal distribution. Thus, a standard normal random variable is a continuous random variable that is used to model a standard normal distribution. The pdf formula is as follows:
f(x) = \(\frac{1}{\sqrt{2\Pi}}e^{-\frac{x^{2}}{2}}\)
Exponential Random Variable
Exponential distributions are continuous probability distributions that model processes where a certain number of events occur continuously at a constant average rate, \(\lambda\geq0\). Thus, a continuous random variable used to describe such a distribution is called an exponential random variable. The pdf is given as follows:
f(x) = λe−λx
Continuous Random Variable vs Discrete Random Variable
Both discrete and continuous random variables are used to model a random phenomenon. The differences between a continuous random variable and discrete random variable are given in the table below:
| Continuous Random Variable | Discrete Random Variable |
|---|---|
| The value of a continuous random variable falls between a range of values. | The value of a discrete random variable is an exact value. |
| The probability density function is associated with a continuous random variable. | The probability mass function is used to describe a discrete random variable |
| A continuous random variable can take on an infinite number of values. | Such a variable can take on a finite number of distinct values. |
| Mean of a continuous random variable is E[X] = \(\int_{-\infty }^{\infty}xf(x)dx\) | The mean of a discrete random variable is E[X] = ∑ x P(X = x), where P(X = x) is the probability mass function. |
| The variance of a continuous random variable is Var(X) = \(\int_{-\infty }^{\infty }(x - \mu )^{2}f(x)dx\) | The variance of a discrete random variable is Var[X] = ∑(x − μ)2 P(X = x) |
| The examples of a continuous random variable are uniform random variable, exponential random variable, normal random variable, and standard normal random variable. | The examples of a discrete random variable are binomial random variable, geometric random variable, Bernoulli random variable, and Poisson random variable. |
Related Articles:
Important Notes on Continuous Random Variable
- A continuous random variable is a variable that is used to model continuous data and its value falls between an interval of values.
- The probability density function of a continuous random variable is given as f(x) = \(\frac{\mathrm{d} F(x)}{\mathrm{d} x}\) = F'(x).
- The cumulative distribution function is given by P(a < X ≤ b) = F(b) - F(a) = \(\int_{a}^{b}f(x)dx\).
- The mean of a continuous random variable is E[X] = \(\mu = \int_{-\infty }^{\infty}xf(x)dx\) and variance is Var(X) = \(\sigma ^{2} = \int_{-\infty }^{\infty }(x - \mu )^{2}f(x)dx\).
- Uniform random variable, exponential random variable, normal random variable, and standard normal random variable are examples of continuous random variables.
FAQs on Continuous Random Variable
What is a Continuous Random Variable in Probability Theory?
A continuous random variable can be defined as a variable that can take on any value between a given interval. These are usually measurements such as height, weight, time, etc.
What is the Expectation of a Continuous Random Variable?
The expectation of a continuous random variable is the same as its mean. The formula is given as E[X] = \(\mu = \int_{-\infty }^{\infty}xf(x)dx\).
What is the Variance of a Continuous Random Variable?
The variance of a continuous random variable is the average of the squared differences from the mean. It is given by Var(X) = \(\sigma ^{2} = \int_{-\infty }^{\infty }(x - \mu )^{2}f(x)dx\).
What are the Types of a Continuous Random Variable?
There are three most commonly used continuous probability distributions thus, there are three types of continuous random variables. These are given as follows:
- Uniform random variable
- Standard normal random variable
- Exponential random variable.
How to Find the CDF of a Continuous Random Variable?
To find the cumulative distribution function of a continuous random variable, integrate the probability density function between the two limits. This is expressed as P(a < X ≤ b) = F(b) - F(a) = \(\int_{a}^{b}f(x)dx\).
What is the Difference Between a Continuous Random Variable and Discrete Random Variable?
A continuous random variable is used for measurements and can have a value that falls between a range of values. A discrete random variable has an exact countable value and is usually used for measuring counts.
What are the Properties of a Continuous Random Variable?
There are two main properties of a continuous random variable. These are as follows:
- The probability density function is integrated to get the cumulative distribution function.
- The variable can be equal to an infinite number of values.