Random Experiments
A random experiment is a type of experiment that has multiple possible outcomes. Such an experiment can be repeated many times. In probability theory, once the random experiment has been performed multiple times then the experimental probabilities of various outcomes can be calculated.
An example of a random experiment is a Bernoulli trial in which there are exactly two possible outcomes. Any outcome of a random experiment cannot be predicted until the experiment has been performed. In this article, we will learn more about a random experiment, its definition, and various associated examples.
| 1. | What are Random Experiments in Probability? |
| 2. | Random Experiments Definition |
| 3. | Random Experiments Example |
| 4. | How to Find Probability of Random Experiments? |
| 5. | FAQs on Random Experiments |
What are Random Experiments in Probability?
A random experiment is a very important part of probability theory. This is because probability theory is based on the assumption that an experiment is random and can be repeated several times under the same condition. An experiment in probability will have a sample space, a set of events as well as the probabilities of occurrence of those events.
Random Experiments Definition
Random experiments can be defined as experiments that can be performed many times under the same conditions and their outcome cannot be predicted with complete certainty. In order words, in a random experiment, all the possible outcomes are known, however, its exact outcome cannot be precisely predicted in advance. There are certain terms associated with random experiments that are given as follows:
- Sample space: A sample space can be defined as the list of all possible outcomes of a random experiment.
- Outcome: An outcome is a possible result of the random experiment.
- Event: An event is a possible outcome of an experiment and forms a subset of the sample space.
- Trial: When a random experiment is repeated many times each one is known as a trial.
Random Experiments Example
Suppose a coin is tossed. The two possible outcomes are getting a head or a tail. The outcome of this experiment cannot be predicted before it has been performed. Furthermore, it can be conducted many times under the same conditions. Thus, tossing a coin is an example of a random experiment.
Another random experiment example is that of rolling a dice. There can be 6 possible outcomes {1, 2, 3, 4, 5, 6}. However, none of the outcomes can be exactly predicted.
How to Find Probability of Random Experiments?
Probability can be defined as the likelihood of occurrence of an outcome of a random experiment. The formula for finding the probability is given as the number of favorable outcomes divided by the total number of possible outcomes of that random experiment. Suppose the probability of getting exactly two heads needs to be determined when a fair coin is tossed twice. The steps to find the probability are as follows:
- Step 1: Determine the sample space of the random experiment or the total number of outcomes. The sample space of a coin tossed twice is given as {HH, HT, TH, TT}. Thus, the total number of outcomes are 4.
- Step 2: Find the number of favorable outcomes. As the probability of getting exactly two heads needs to be determined the number of favorable outcomes is 1.
- Step 3: Apply the probability formula. Thus, the probability of getting two heads is 1 / 4 or 0.25.
Related Articles:
Important Notes on Random Experiments
- A random experiment is an experiment whose outcome cannot be predicted.
- A random experiment can be performed several times under the same condition.
- The probability of a random experiment can be given by the number of favorable outcomes / total number of outcomes.
Examples on Random Experiments
-
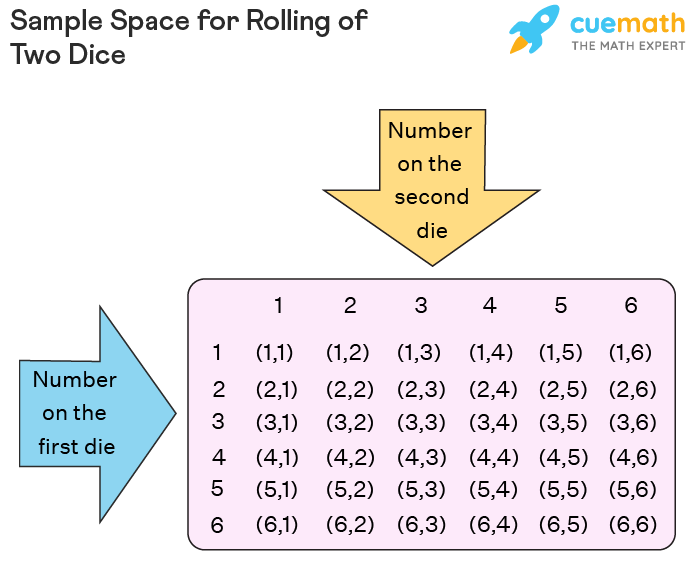
Example 1: What is the sample space for the random experiment of rolling two dice?
Solution: The sample space is given as follows:
S = {(1, 1) , (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
FAQs on Random Experiments
What are Random Experiments?
Random experiments are experiments that can be performed several times and the outcome cannot be predicted beforehand.
What is the Random Experiment Sample Space and Event?
A sample space of a random experiment enlists all the possible outcomes of that experiment. However, an event is a set of possible outcomes of a random experiment that is a subset of the sample space.
What are the Two Conditions that Random Experiments Must Satisfy?
For experiments to be random experiments they must satisfy the following two conditions:
- The experiment can be arbitrarily repeated many times under the same conditions.
- The outcome of each trial of a random experiment cannot be predicted before the experiment has been performed.
What is the Formula to Find the Probability of an Outcome of a Random Experiment?
The likelihood of occurrence of any outcome of a random experiment can be calculated by the formula number of favorable outcomes / total number of outcomes.
What are the Steps to Find the Probability of a Random Experiment?
To find the probability of an outcome the steps are as follows:
- Find the total number of outcomes of the random experiment.
- Find the number of favorable outcomes.
- Divide step 2 by step 3 to determine the probability.
Can Dividing 20 by 5 Be Considered a Random Experiment?
On diving 20 by 5 the outcome will always be 4. Thus, as the outcome is predictable this cannot be classified as a random experiment.
What is a Random Variable and a Random Experiment?
A random variable is a variable that can assume all possible outcomes of a random experiment and its value changes with every trial that is performed.