Exponential Growth Formula

Before knowing the exponential growth formula, first, let us recall what is meant by exponential growth. In exponential growth, a quantity slowly increases in the beginning and then increases rapidly. We use the exponential growth formula in finding the population growth, finding the compound interest, and finding the doubling time. Let us understand the exponential growth formula in detail in the following section.

Meaning of Exponential Growth Formula 

Exponential growth is a pattern of data that shows an increase with the passing of time by creating a curve of an exponential function. For example, suppose a population of cockroaches rises exponentially every year starting with 3 in the first year, then 9 in the second year, 729 in the third year, 387420489 in the fourth year, and so on. The population is growing to the power of 3 each year in this case. The exponential growth formula, as its name suggests, involves exponents. There are multiple formulas involved with exponential growth models. They are:

Formula 1: f(x) = ab^x

Formula 2: f(x) = a (1 + r)^x

Formula 3: P = P\(_0\) e^{k t} 

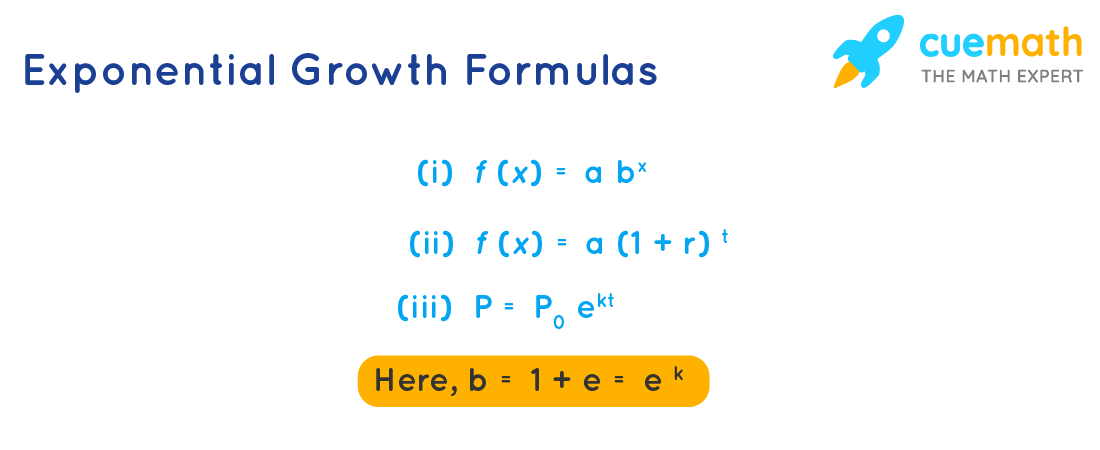
Exponential Growth Formulas 

Formula 1: f(x) = ab^x

Formula 2: f(x) = a (1 + r)^x

Formula 3: P = P\(_0\) e^{k t} 

Where, 

• a (or) P\(_0\) = Initial value
• r = Rate of growth
• k = constant of proportionality
• x (or) t = time (time can be in years, days, (or) months, whatever you are using should be consistent throughout the problem).

Note: Here, b = 1 + r ≈ e^k. In exponential growth, always b > 1.

Examples Using Exponential Growth Formula 

Example 1: There were 50 fishes in a pond. They had increased to 135 after six months. If the fishes are growing exponentially, then how many fishes will there be in the pond at the end of one year? Round your answer to the nearest integer.

Solution:

The initial number of fishes is a = 50.

Since the fishes increased exponentially, we use the exponential growth formula.

y = a b^x

y = 50 b^x ... (1)

It is given that the number of fishes after 6 months is 135. So we substitute x = 1/2 (half-year) and y = 135 in the above equation.

135 = 50 (b)^½

Dividing both sides by 50,

2.7 = b^½

Squaring on both sides,

7.29 = b

Here, you can observe that b = 7.29 > 1, as it is exponential growth.

We have to find the number of fishes at the end of 1 year. So we substitute x = 1 and b = 7.29 in (1).

y = 50 (7.29)¹ = 364.5 ≈ 365 (Rounded to the nearest integer).

Can you try this problem using any other formula of exponential growth?

Therefore, the number of fishes at the end of one year = 365.

Example 2: Jake lends $20,000 to his friend at an annual interest rate of 5.7%, compounded annually. Using the exponential growth formula, find the amount owed by his friend after 6 years? Round your answer to the nearest integer.

Solution:

The initial amount is a = $20,000.

r = rate of interest (growth) = 5.7% = 5.7/100 = 0.057.

x = number of years = 6 (we took the number of "years" here because the given rate is the "annual" rate).

By using the exponential growth formula,

f(x) = a (1 + r)^x

f(x) = 20000 (1 + 0.057)⁶ ≈ 27,892 (Rounded to the nearest integer).

Therefore, the total amount owed after 6 years = $27,892.

Example 3: In 2001, there were 100 inhabitants in a remote town. Population has increased by 10% every year. How many residents will there be in 5 years?

Solution: 

Given, 

a = 100

r = 10% = 0.10

x = 5

Using the exponential growth formula, 

f(x) = a (1 + r)^x

f(x) = 100(1 + 0.10)⁵

f(x) = 161.051 = 162 (rounded to the nearest integer) 

Therefore, the number of residents in 5 years will be 162.