Length Width Height
The length, width and height are the dimensions of a geometrical figure that depict how long, wide and high a figure is. While length is the longest side of a figure, width is the shorter side and height is the vertical dimension of the figure. Let us learn more about the length width height of figures.
| 1. | What is Length Width Height? |
| 2. | Length vs Width |
| 3. | Length Width Height of a Box |
| 4. | FAQs on Length Width Height |
What is Length Width Height?
Length, width, and height are the tools that are used to find the dimensions of an object. When we refer to two-dimensional shapes (2D shapes), we use the length and width, whereas when we refer to three-dimensional shapes (3D shapes) we use the height along with the length and width. Let us understand the three terms now.
- Length: Length is used to measure the distance between two points. Length is the longest dimension of a figure and it shows how long the given object or figure is. It is expressed in linear units like meters, centimeters, inches, and so on.
- Width: Width is the shorter distance of an object or a figure and it shows how broad or wide the given figure is. Width is also expressed in linear units like meters, centimeters, inches, and so on.
- Height or Depth: The height of an object refers to its depth or the third vertical dimension of the object and it shows how high or deep an object is. The height or depth of an object is expressed in linear units like meters, centimeters, inches, and so on.
It should be noted that length, width, height and depth are words that are derived from the words long, wide, high, and deep, respectively. Hence they express the dimensions of an object. Observe the figure given below to see the length width and height of a cuboid.
Length vs Width
The difference between the length and width of a figure is that length signifies the longer side and width signifies the shorter side of a figure.
The length shows how long the figure is and the width shows how broad or wide it is. The width is also referred to as breadth. For example, if the two sides of a rectangle are given as 8 cm and 3 cm, we can easily identify that the length of the rectangle is 8 cm and the width of the rectangle is 3 cm. Observe the rectangle given below to see the difference between the length and width of a shape.
Length x Width x Height
The length width and height are usually used together to find the volume of a geometrical figure like a rectangular prism which is also known as a cuboid. When we multiply the length, width, and height of a cuboid, we get its volume. This means, Length x Width x Height = Volume of Cuboid. In other words, the capacity or volume of a cuboid or any rectangular box can be measured if we multiply these three dimensions together. Let us understand this with an example.
Example: Find the volume of a cuboid if its length is 8 units, width is 4 units, and height is 3 units.
Solution: The volume of a cuboid can be calculated using the formula,
Volume of Cuboid = Length x Width x Height
After substituting the values we get, Volume of Cuboid = 8 × 4 × 3 = 96 units3
Length Width Height of a Box
The length, width and height of a box can be easily identified because we know that length is the longest side, width is the shorter side and height is the vertical dimension of the box. Observe the figure given below which shows the length, width and height of a box.
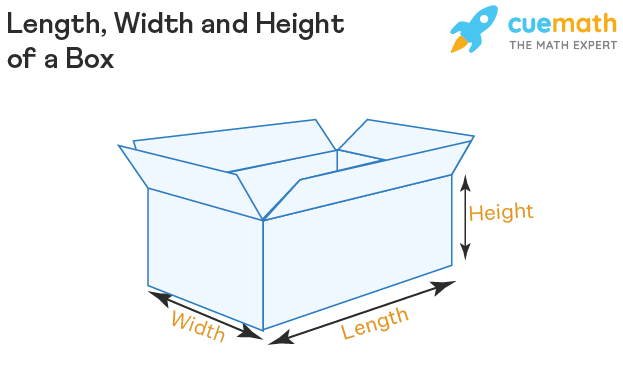
These dimensions are always expressed in the order where the length comes first, followed by the width and then the height. This means if the dimensions of a box are to be measured they are expressed in the order of length, width and height. For example, 15'' × 10'' × 3'' means 15'' is the length of the box, 10'' is the width of the box and 3'' is the height of the box.
☛Related Articles
FAQs on Length Width Height
What is Length Width Height?
Length, width, height, and depth are words that are derived from the adjectives long, wide, high, and deep, respectively. Hence, they express the dimensions of an object. While length shows how long the given object is, the width shows how broad it is and height shows how high it is. All these are expressed in linear units like centimeters, meters, inches, and so on.
What is the Formula for Length Width and Height?
When the length, width, and height of a cuboid are multiplied together, it gives the volume of the cuboid. The formula for the volume of a cuboid is, Volume of Cuboid = Length × Width × Height.
What is the Difference Between Length Width Height?
The length, width, height of an object are the different dimensions expressed in linear units. While length is the longest side of a shape, width is the shorter side, and height is the vertical dimension or depth of the shape.
What is the Order of Length Width Height?
When the dimensions of a geometrical figure are written, they are written in the order in which the length comes first, followed by the width and then the height. For example, if the dimensions of a cuboid are to be expressed, it will be written as Length × Width × Height, that is, 7 × 4 × 3, where 7 represents the length, 4 represents the width and 3 represents the height of the cuboid.
How to Calculate Cubic meter from Length Width Height?
Cubic meter is the unit that expresses the volume of a cuboid. Therefore, in order to find the volume of a cuboid in cubic meters the length, width and height are multiplied together. It should be noted that all the length, width and height should have the same units (meters) so that the volume is expressed in cubic meters. For example, if the length of a cuboid is 10 m, its width is 6 m and height is 3 m, let us find its volume in cubic meters. Volume of a cuboid = length × width × height. After substituting the values, we get, Volume of a cuboid = 10 × 6 × 3 = 180 cubic meters.
What is the Length Breadth and Height of a Cuboid?
The length of a cuboid is the longest side when the cuboid is placed horizontally. The width is the shorter side of the cuboid. The height is the vertical dimension of the cuboid.
How to Find the Length Width and Height when Volume is Given?
The formula that is used to find the volume of a cuboid is, Volume of Cuboid = Length × Width × Height. Therefore, if any one dimension is missing, it can be calculated by using this formula by substituting the other given values. For example, let us find the height of a cuboid if the volume of a cuboid is given as 144 cubic cm, the length = 12 cm, width = 2 cm. Since the height of the cuboid is not known, let us substitute the rest of the dimensions in the formula. Volume of Cuboid = Length × Width × Height. After substituting the known values we get, 144 = 12 × 2 × Height. After solving this we get the height as, 6 cm.