Repeating Decimal to Fraction
It is very easy to convert a terminating decimal to a fraction, but how do we convert a repeating decimal to fraction? Repeating decimals are decimal numbers that do not terminate after a finite number of digits and in these numbers, one or more digits repeat themselves again and again. For example 34.56565656... Repeating decimal to fraction conversion can be done by following some simple steps given below.
| 1. | How to Convert Repeating Decimal to Fraction? |
| 2. | Repeating Decimal to Fraction Trick |
| 3. | Repeating Decimal to Fraction Chart |
| 4. | FAQs on Repeating Decimal to Fraction |
How to Convert Repeating Decimal to Fraction?
Repeating or recurring decimals are those decimal expansions that do not terminate or end after a specific number of digits. Such numbers have an infinite number of digits after the decimal point. And there is a repetitive pattern in those digits.
Generally, decimal numbers can be converted to fractions by dividing the number with a power of 10 which is equal to the number of decimal places. For example, 1.5 = 15/10 = 3/2. But with repeating decimals, it is impossible to count the number of decimal places as it is infinite. So, there are some specific steps to be followed to convert repeating decimal to fraction. The repeating decimal to fraction steps of conversion are given below:
- Step 1: Identify the repeating digits in the given decimal number.
- Step 2: Equate the decimal number with x or any other variable.
- Step 3: Place the repeating digits to the left of the decimal point by multiplying the equation obtained in step 2 by a power of 10 equal to the number of repeating digits. This way you will get another equation.
- Step 4: Subtract the equation obtained in step 2 from the equation obtained in step 3.
- Step 5: Simplify to get the answer.
Let us take an example to understand the conversion of repeating decimal to fraction in a better way. Convert 0.77777... to a fraction.
Step 1: We can observe that 7 is repetitive in the given decimal number.
Step 2: Let x = 0.7777...
Step 3: There is only 1 repetitive digit, so multiply this equation by 10. We get, 10x = 7.7777...
Step 4: Subtract x = 0.7777... from 10x = 7.7777... We will get 9x = 7.
Step 5: x = 7/9. Therefore, 0.7777... = 7/9.
When we consider the conversion of repeating decimal to fraction, there are two types of repeating numbers that come up. Those are given below:
- Numbers with only repeating digits, for example, 0.222..., 0.999..., 0.787878..., etc.
- Numbers with multiple digits, for example, 2.7646464..., 98.735735735..., etc
We have already discussed how to convert the first type of repeating decimals to fractions. Now, let us convert a multi-digit repeating decimal to fraction. Convert 3.989898... to a fraction.
Step 1: The repeating digits in the given decimal number are 98.
Step 2: Let x = 3.989898...
Step 3: Since there are two repeating digits, multiply the above equation by 100. We will get, 100x = 398.989898...
Step 4: Subtract x = 3.989898... from 100x = 398.989898... We will get 99x = 395.
Step 5: x = 395/99. Therefore, 3.989898... = 395/99.
Let us take one more example in which we would need to make three equations in order to convert the number to a fraction. Convert 2.7646464... to a fraction.
Let us first equate it to a variable, x. So, x = 2.7646464... Now, the repeating digits are 64. So, let us multiply this equation by 10 such that we will have repeating digits after the decimal point. It implies, 10x = 27.6464...
10x = 27.6464... (equation 1)
Now, let us multiply x = 2.7646464... by 1000 so that we will have decimal point to the right of the repeating digits.
1000x = 2764.6464... (equation 2)
Subtract equation 1 from equation 2, we will get,
1000x - 10x = (2764.6464...) - (27.6464...)
990x = 2737
x = 2737/990
Therefore, 2.7646464... = 2737/990.
Repeating Decimal to Fraction Trick
An easy trick to convert a repeating decimal to the fraction form is to write the repeating digits as the numerator over the same number of 9s. Some examples of repeating decimal to fraction are given below:
- 0.444... = 4/9 (as there is only 1 repeating digit 4, so only one 9 will come in the denominator)
- 0.787878... = 78/99 (as there are 2 repeating digits 7 and 8, so two times 9, i.e 99 will come in the denominator)
- 0.999... = 9/9 = 1
Note that this trick is only applicable for repeating decimals with only the repeating digits. There should not be any other digit present in the given number. In that case, we need to use the repeating decimal to fraction steps of conversion explained above.
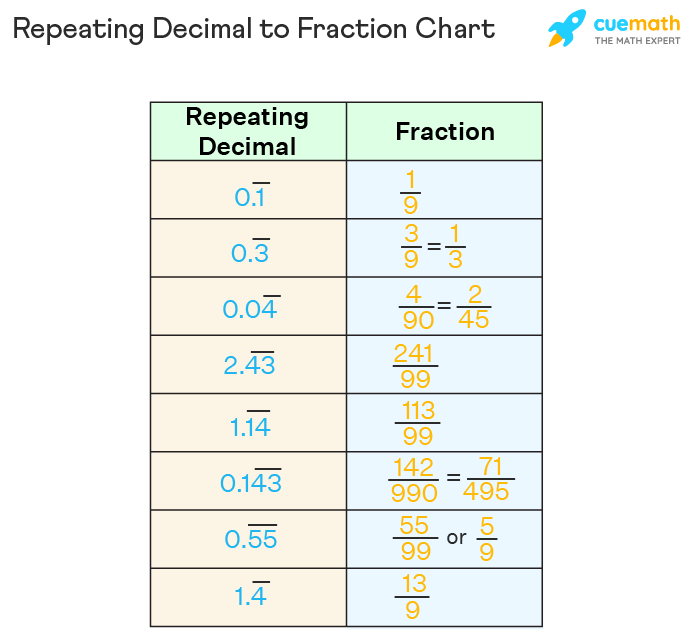
Repeating Decimal to Fraction Chart
A repeating decimal to fraction chart will help you to get the fractional values of some commonly used repeating decimals. You can try to convert the repeating decimals (written on the left) to fractions and then use the chart below to verify your answers.
Related Articles
Check these interesting articles related to the concept of repeating decimal to fraction in math.
Repeating Decimal to Fraction Examples
-
Example 1: Convert 1.888... to fraction.
Solution: The given decimal number is a repeating decimal, and we have to convert repeating decimal to fraction form. To do that, we need to have two equations - one with the repeating digits on the right of the decimal point and the other with a decimal point to the right of the repeating digit(s). Let x = 1.888... be equation 1.
Multiplying equation (1) by 10, we get,
10x = 18.888... (equation 2)
Subtract equation (1) from equation (2),
9x = 17
x = 17/9
Therefore, 1.888... = 17/9.
-
Example 2: What fraction is equivalent to the repeating decimal number 0.414141...?
Solution: To convert the given repeating decimal to fraction, we need to follow the steps given below:
- Let a = 0.414141... (equation 1)
- Multiply equation (1) by 100, we get, 100a = 41.414141... (equation 2)
- Subtract equation (1) from (2), we get, 99a = 41.a = 41/99
- Therefore, 0.414141... = 41/99.
You can also try finding the answer by using the repeating decimal to fraction trick explained above.

FAQs on Repeating Decimal to Fraction
What is Converting Repeating Decimal to Fraction?
Converting repeating decimal to fraction means finding the fractional equivalent of a decimal expansion which is recurring or repeating. We can easily convert a fraction to a repeating decimal by dividing the numerator with the denominator. But to convert a repeating decimal to fraction, we need a specific procedure to follow.
How to Change Repeating Decimal to Fraction?
To change a repeating decimal to a fraction, follow the steps mentioned below:
- Identify the set of repeating digits in the given decimal number.
- Make two equations - one with a decimal point on the left of the repeating digits and the other with the decimal point to the right of the first set of repeating digit(s).
- To do that, equate the given number to any variable and multiply the equation with a suitable power of 10.
- After that, we subtract the smaller equation from the larger one to get the fractional equivalent of the given repeating decimal.
How to Express Non-Terminating Repeating Decimal to Fraction?
Non-terminating repeating decimals and repeating decimals are the same, as all repeating decimals are non-terminating as well. To express a non-terminating repeating decimal to a fraction, we need to follow the same steps as we do while converting a repeating decimal to fraction.
What is 0.22... Repeating Decimal to Fraction?
In the given number 0.22... there is one repeating digit which is 2. So, by using the repeating decimal to fraction trick, we know that 0.22... can be written as 2/9.
What are the Steps to Convert a Repeating Decimal to a Fraction?
The steps to convert a repeating decimal to a fraction are given below:
- Identify the repeating digits in the given number.
- Equate the number with any variable.
- Multiply both sides of the equation by a power of 10 such that the decimal point will come to the right of the repetitive digit.
- If needed, find one more equation such that all the repeating digits will be at the right of the decimal point.
- Subtract the smaller equation from the larger equation.
This is the method to convert a repeating decimal to a fraction.
visual curriculum