Secant Formula

When talking about any right-angled triangle, there are three sides that are, hypotenuse, perpendicular, and height. The side which is the largest one and is on the side which is on the opposite to the right angle is the hypotenuse. When the length of the hypotenuse is divided by the length of the adjacent side, it gives the secant of the angle, of the right-angled triangle. Secant is denoted as 'sec'. Secant formula is derived out from the inverse cosine (cos) ratio. The secant function is the reciprocal of the cosine function, thus, the secant function goes to infinity whenever the cosine function is equal to zero (0). The secant formula along with solved examples is explained below.

What is Secant Formula?

In the right-angled triangle, there are three sides i.e. Hypotenuse, the Perpendicular side (opposite), and the Adjacent side which is the height. The largest side in the triangle is the hypotenuse, the side opposite to the angle is the perpendicular side, and the side where both hypotenuse and opposite rests is the adjacent side.

The secant function of a right triangle is its hypotenuse divided by its base. Thus, the secant formula of a given triangle can be expressed as,

sec ⁡θ = H/B

Where,

• B = Base
• H = hypotenuse

Also, secant is reciprocal of cos,i.e.,

sec θ = (1/cosθ)

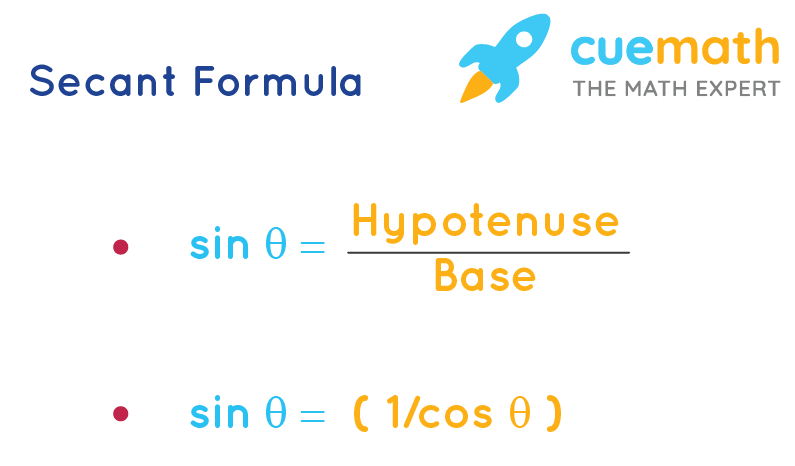
For the secant of an angle, there is a formula related to the Pythagoras theorem, i.e. 

Sec² ⁡θ = 1 + tan² ⁡θ 

Note: This equation is very useful. It is similar to the squared relationship between sin ⁡θ and cos ⁡θ. (i.e. Sec² ⁡θ - tan² ⁡θ  = 1)

Examples Using Secant Formula

Example 1: Find the side of a right-angled triangle whose hypotenuse is 14 units and base angle with the side is 60 degrees.

Solution: 

Given,

θ = 60 degree
H = 14 units

Using the secant formula,

sec⁡θ = H/B

sec⁡60 =14/B

2 = 14/B

B = 14/2

B = 7

Therefore, the base side of a right-angle triangle is 7 Units.

Example 2: Find sec θ using the secant formula if hypotenuse = 4.9 units, the base of the triangle = 4 units, and perpendicular = 2.8 units. 

Solution:

Given: P = 2.8, B = 4, and H = 4.9

Using the secant formula,

sec⁡θ = H/B

sec⁡θ = 4.9/4

sec⁡θ = 1.225

Therefore, sec θ is 1.225

Example 3: Find Secθ if Cosθ is given as 4/8 using a secant formula.

Solution:

Given, Cos θ = 4/8 = 1/2

Using the reciprocal secant formula, 

sec θ = (1/cosθ)

sec θ = 1/½

sec θ = 2

Therefore, sec θ is 2.