Square Root by Long Division Method
The most commonly used method to find the square root of a number is the division method. In this article, we will learn how to solve square root problems using the division method for perfect square numbers and non-perfect square numbers.
| 1. | Square Root of a Perfect Square by Long Division Method |
| 2. | Square Root of a Non - Perfect Square by Long Division Method |
| 3. | FAQs on Finding Square Root of a Number by Division Method |
Square Root of a Perfect Square by Long Division Method
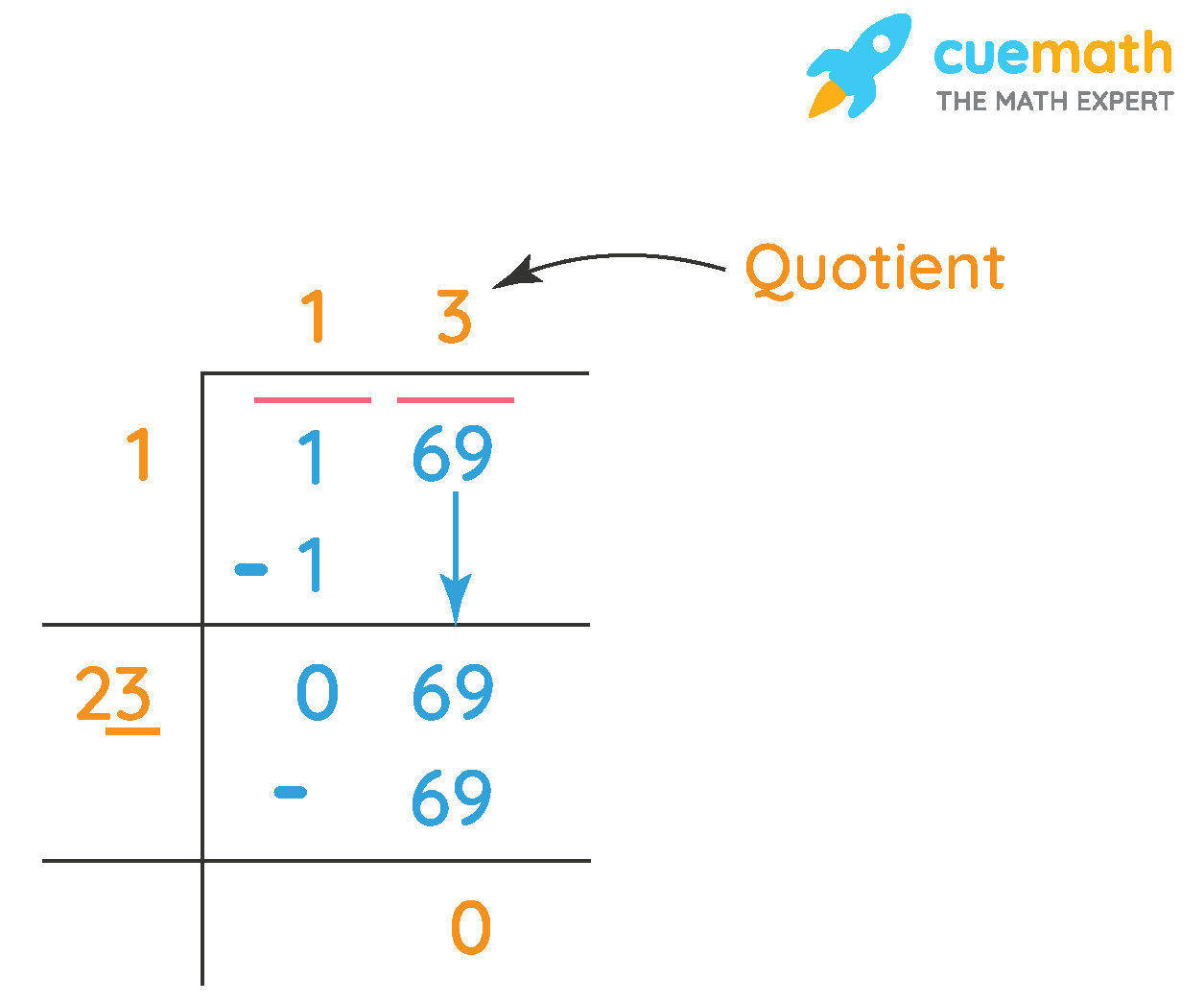
Finding the square root by division method is a very familiar and easy method to get the accurate square root of numbers. In this method, there are 5 main operations that are used- divide, multiply, subtract, bring down and repeat. Let us look at the following example of a perfect square number 169. Follow the steps and relate them with the image given below.
- Step 1: Write the number 169 inside the division symbol below the division bar.
- Step 2: Make pairs of 2 digits from the right-hand side. In this case, 69 is one pair leaving 1 stand alone.
- Step 3: Now think of a number and divide 1 with such a number so that it gives 1 or a number less than 1.
- Step 4: Here, we get 0 as the remainder and 1 as the quotient.
- Step 5: Now bring down pair 69 as the next dividend to complete the method.
- Step 6: The quotient obtained in the previous step is 1. According to square root rules, we need to double the quotient to get the next divisor. So, multiply the quotient 1 by 2 (1 × 2 = 2) and place 2 as the next divisor which needs to be paired.
- Step 7: Find a divisor "p" such that p × p results in the product ≤ 69. Think of a number that can be paired up with 2 and become a two-digit new divisor.
- Step 8: Now, we get our new divisor as 23. Divide 69 ÷ 23 = 3, which gives 3 as the next quotient and we get the remainder as 0.
- Step 9: Therefore, 13 is the square root of 169.
Square Root of a Non-Perfect Square by Long Division Method
To find the square root of a non-perfect square number, we use the following steps. Let us take an example of the number 128.
- Step 1: Write the number 128 and make pairs of 2-digits from the right. Here, 1 is left alone.
- Step 2: Think of a number with which we can divide 1. If we divide the number 1 by 1 and we get the remainder as 0 with quotient = 1.
- Step 3: Bring down the next pair of numbers which is 28. Now, the new dividend is 28.
- Step 4: According to square root rules, we need to double the quotient to get the next divisor. We will have 2 in the new divisor's place.
- Step 5: Think of a number that can be paired up with 2 and become a two-digit new divisor.
- Step 6: If the number 1 is paired up with 2 it makes a 2 digit number 21. On multiplying 21 by 1 we get 21, which is less than 28. (21 × 1 = 21).
- Step 7: On subtracting 28 - 21, we get the remainder = 7.
- Step 8: Now, place a decimal after 11 and place 3 pairs of zeros after the dividend 128 to continue the division.
- Step 9: Bring down one pair of zeros. Now, we have the new dividend as 700.
- Step 10: On repeating the steps from step 5, we have the new divisor as 22. Now, again think of a number to be paired up with 22 to get a 3-digit new divisor such that the new divisor multiplied with that number gives the product which is ≤700. (223 × 3 = 669).
- Step 11: Now repeat the process until you get the repetition of the digits as a recurring quotient.

The square root of 128 by long division method is 11.313.
Related Articles on Finding Square Root of a Number by Division Method
Check out these interesting articles to know more about finding the square root of a number by the division method.
Solved Examples on Finding Square Root of a Number by Division Method
-
Example 1: Find the square root of 68 by division method.
Solution:
To find the square root of a number 68 by long division method we will follow the same procedure as shown above. The division looks like this:

The square root of 68 by long division method is 8.246
-
Example 2: Find the least number that must be subtracted from 5630 so as to get a perfect square. Try to find the square root of the perfect square using the division method.
Solution: Let us find the square root of 5630 using the division method.
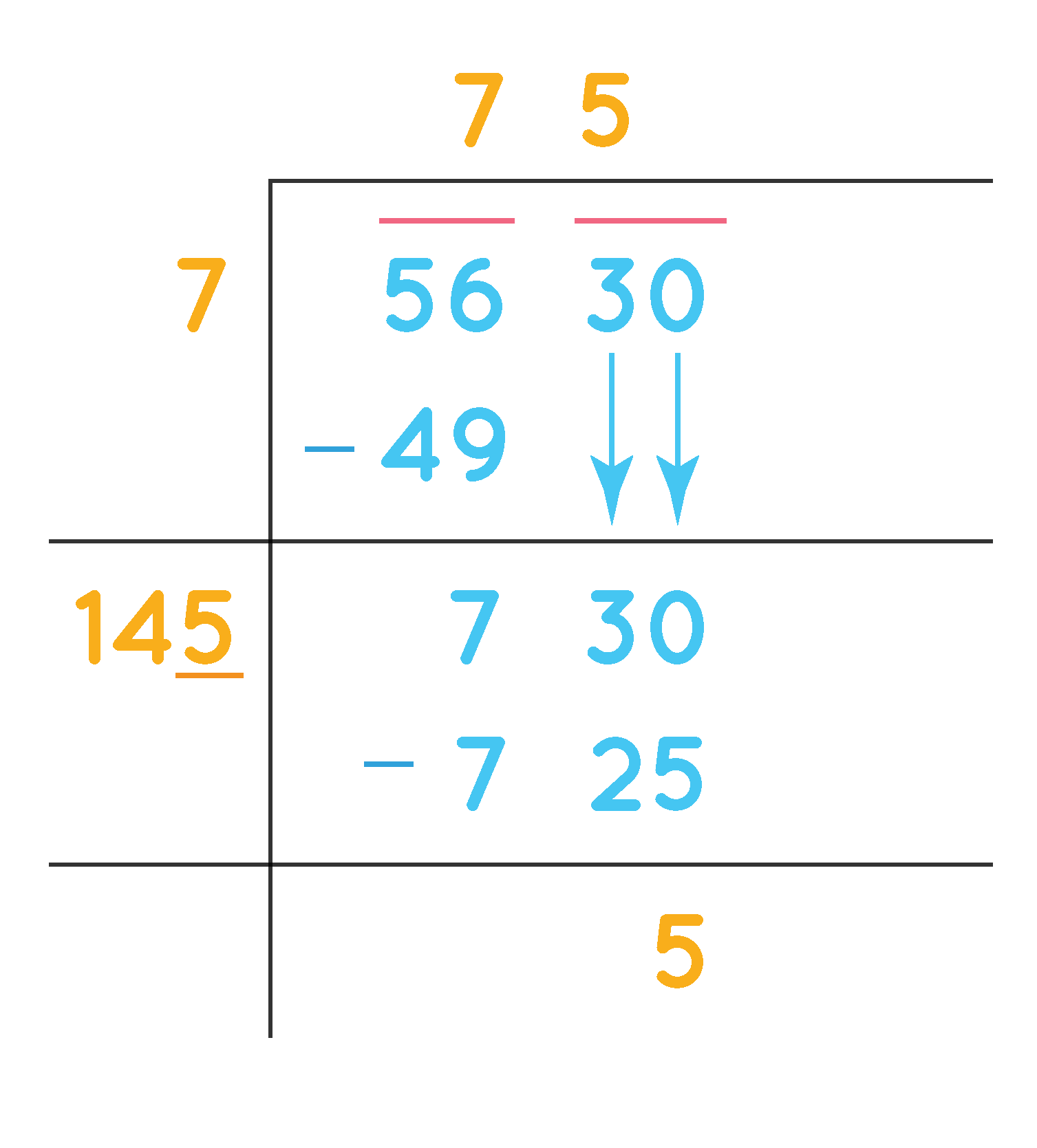
We get the remainder as 5. It proves that 75² < 5630.
On subtracting the remainder 5 from the given number 5630 we get a perfect square. Therefore, the perfect square is 5630 - 5 = 5625.
The square root of 5625 using the division method is 75.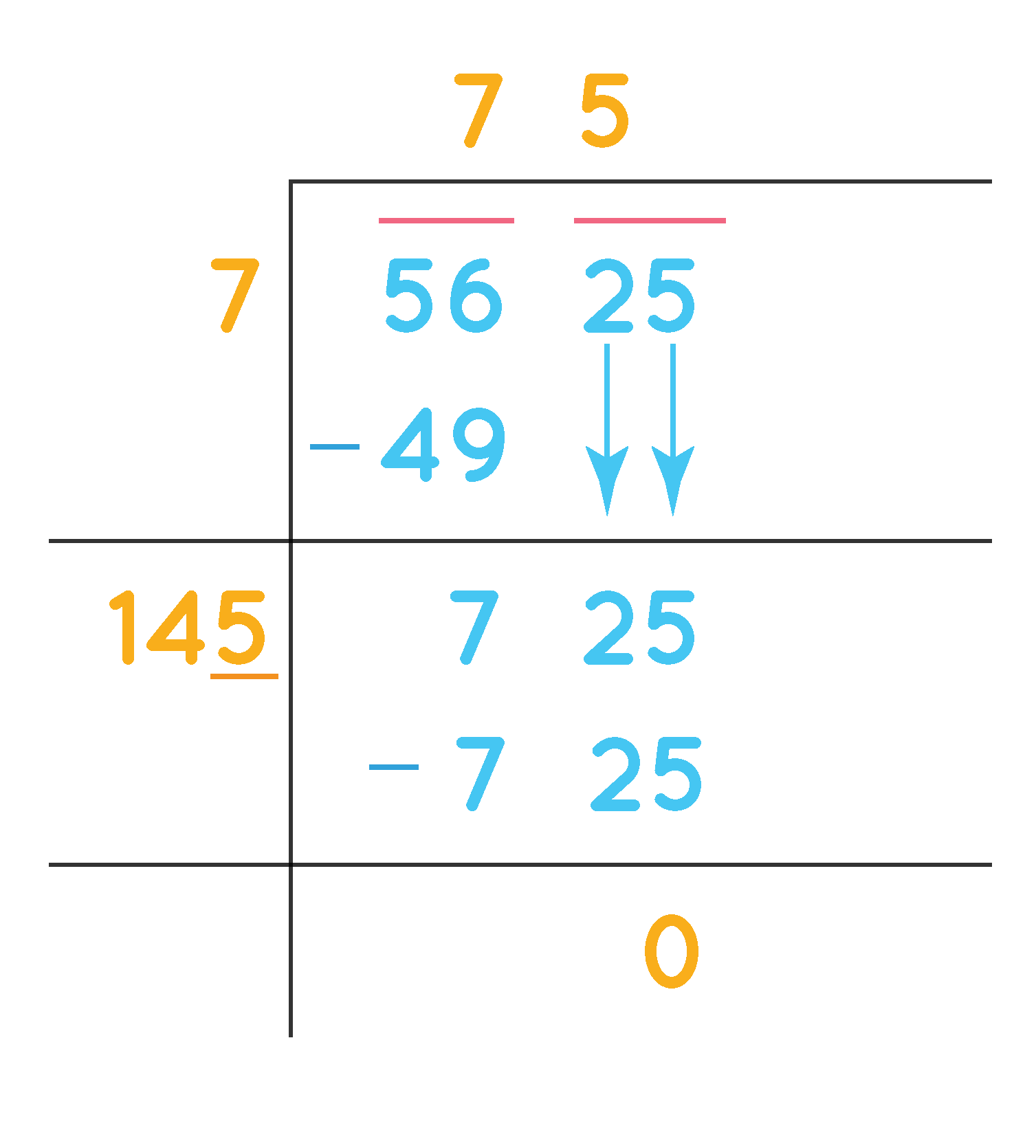
-
Example 3: Find the least number that must be added to 1304 so as to get a perfect square. Try to find the square root of the perfect square using the division method.
Solution: Let us find the square root of 1304 using the division method.

We get the remainder as 8. It proves that 36² < 1304.
The next number which is a perfect square is 37² = 1369.
The required number to be added in 1304 is 1369 - 1304 = 65
1304 + 65 = 1369
Therefore, the square root of 1369 using the division method is 37.

Practice Questions on Finding Square Root of a Number by Division Method
FAQs on Finding Square Root of a Number by Division Method
How to Find the Square Root of Non Perfect Squares?
The easiest way to find the square root of a non perfect square is the division method. It gives the value in decimals which can be rounded off as per the requirement.
How to Find the Square Root of a Decimal Number by Division Method?
The square root of a decimal number can be calculated by using the long division method. In this case, we make pairs of the whole number parts and the fractional parts and then follow the same process of long division.
What is the Square Root Symbol?
The symbol that is used to denote the square root of a number is √ . It is also known as the radical sign.The number inside the radical sign is known as the radicand. For example, in √81 = 9; the radicand is 81 and 9 is the square root.
What is the Square Root of 2?
Since 2 is not a perfect square we use the long division method to calculate its square root. The square root of 2 is 1.414 up to 3 decimal places.
What are Square Roots?
The square root of a number is the value which when multiplied by itself gives the original number. For example, the square root of 64 is 8 because when 8 is multiplied by itself it gives 64. It is written as √64 = 8.
visual curriculum