Square Root of 83
The square root of 83 is expressed as √83 in the radical form and as (83)½ or (83)0.5 in the exponent form. The square root of 83 rounded up to 6 decimal places is 9.110434. It is the positive solution of the equation x2 = 83.
- Square Root of 83: 9.1104335791443
- Square Root of 83 in exponential form: (83)½ or (83)0.5
- Square Root of 83 in radical form: √83
| 1. | What is the Square Root of 83? |
| 2. | Is Square Root of 83 Rational or Irrational? |
| 3. | How to Find the Square Root of 83? |
| 4. | Important Notes |
| 5. | FAQs on Square Root of 83 |
| 6. | Challenging Questions |
What is the square root of 83?
The square root of a number n is written as √n. This number when squared or multiplied by itself results in the original number n. The square root of 83 can be written in multiple ways
- Radical form: √83
- Decimal form: 9.11
- Exponent form: (83)1/2
Is Square Root of 83 Rational or Irrational?
- 83 is a number that is not a perfect square, meaning it does not have a natural number as its square root.
- Also, its square root cannot be expressed as a fraction of the form p/q which tells us that the square root of 83 is an irrational number.
How to Find the Square Root of 83?
There are multiple ways to find the square root of 83-
- Long Division Method
- Estimation and Approximation
One can find out more about these methods by clicking here
Long Division Method
The square root of 83 by long division method consists of the following steps:
- Step 1: Starting from the right, we will pair up the digits 83 by putting a bar above them. We also pair the 0s in decimals in pairs of 2 from left to right.
- Step 2: Find a number that, when multiplied to itself, gives a product less than or equal to 83. The number 9 fits here as 9 square gives 81. Dividing 83 by 9 with quotient as 9, we get the remainder as 2.
- Step 3: Drag a pair of 0’s down and fill it next to 2 to make the dividend 200.
- Step 4: Double the divisor 9, and enter 18 below with a blank digit on its right. Guess the largest possible digit(X) to fill in the blank and the quotient for which the product of 18X × X results in a value less than or equal to 200. This will be 1 in this case, so divide 200 with 181 and write the remainder.
- Step 5: Repeat this process to get the decimal places you want.
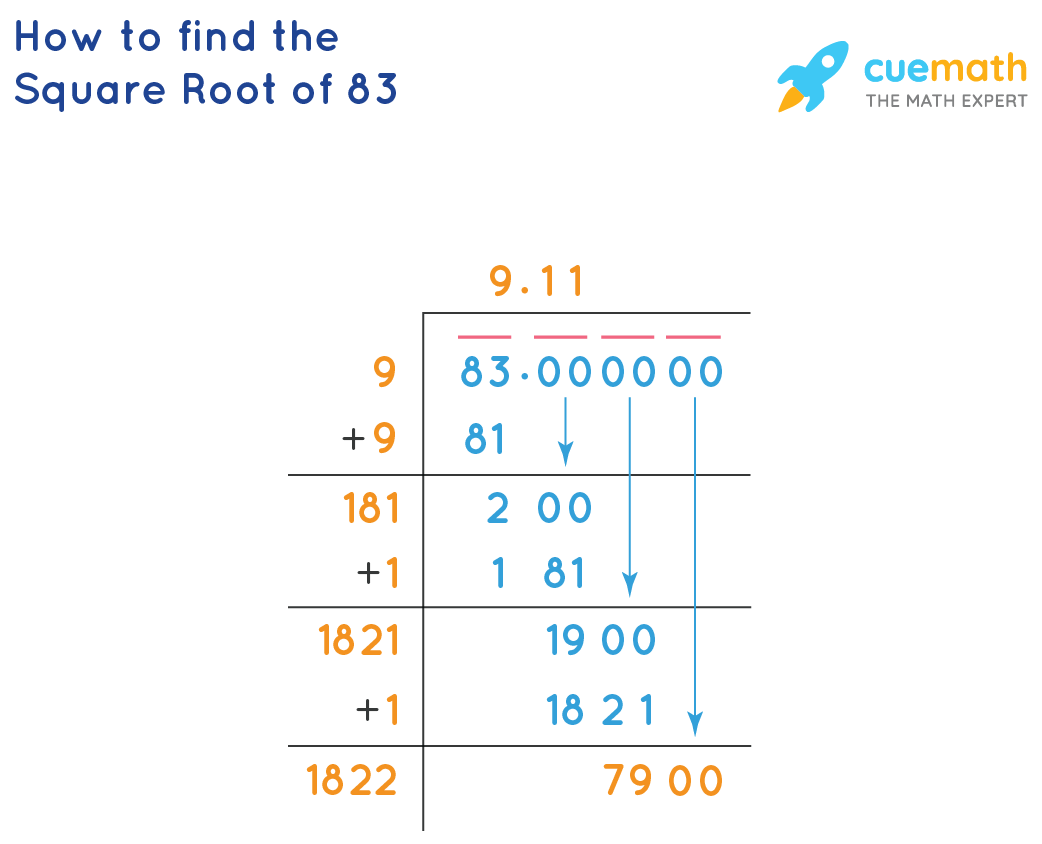
Therefore, the square root of 83 = 9.11
Estimation and Approximation
The estimation method gives us an approximate answer and is usually not accurate to more than 1 decimal place. However, it is easy to perform as can be seen under.
- Step 1: Find a perfect square that is smaller than and bigger than 83. In this case, 9 and 10 will work as their squares are 81 and 100.
- Step 2: Writing in terms of inequality- 9<√83<10 = 81<83<100
- Step 3: Multiply by 100 and write in terms of square roots- √8100<√8300<√10000
- Step 4: Move closer to inequality- √8281<√8300<√8464 = 91<10√83<92
= 9.1<√83<9.2 - Step 5: Taking average of upper and lower limits we get, (9.1 + 9.2)/2 = 9.15
Therefore, we can estimate the square root of 83 ≅ 9.15
Explore Square roots using illustrations and interactive examples
Important Notes
- The square root of 83 is an irrational number.
- The number 83 is not a perfect square.
- There will be n/2 digits in the square root of an even number with n digits.
- There will be (n+2)/2 digits in the square root of an odd number with n digits.
Challenging Questions
- What is the square root of 83 up to 5 decimal places(Use Long Division)
- What are the roots of -83? Also, find the value of the square of the negative root of -83
Solved Examples
-
Example 1:
Sam was wondering whether the value of -√83 is the same as √-83. What do you think?
Solution
Negative square roots cannot be real numbers.
-√83 is a real number, but √-83 is an imaginary number.
Hence, they are not the same, and -√83 is not the same as √-83. -
Example 2:
Andy is travelling down the highway at an average speed of 5√83 km/hr for exactly 1 hour. How much distance does he cover?
Solution
We need to use the formula Distance = Speed * Time
Speed = 5√83 = 45.552 km/hr
Time = 1 hr
Using the formula, Distance = 45.552 * 1 = 45.552Therefore, Andy covers a distance of 45.552 km
-
Example: If the area of a square is 83 in2. Find the length of the side of the square.
Solution:
Let 'a' be the length of the side of the square.
⇒ Area of the square = a2 = 83 in2
⇒ a = ±√83 in
Since length can't be negative,
⇒ a = √83 = 9.110 in

FAQs on the Square Root of 83
What is the Value of the Square Root of 83?
The square root of 83 is 9.11043.
Why is the Square Root of 83 an Irrational Number?
The number 83 is prime. This implies that the number 83 is pairless and is not in the power of 2. Therefore, the square root of 83 is irrational.
What is the Square Root of -83?
The square root of -83 is an imaginary number. It can be written as √-83 = √-1 × √83 = i √83 = 9.11i
where i = √-1 and it is called the imaginary unit.
What is the Value of 17 square root 83?
The square root of 83 is 9.110. Therefore, 17 √83 = 17 × 9.110 = 154.877.
What is the Square of the Square Root of 83?
The square of the square root of 83 is the number 83 itself i.e. (√83)2 = (83)2/2 = 83.
If the Square Root of 83 is 9.110. Find the Value of the Square Root of 0.83.
Let us represent √0.83 in p/q form i.e. √(83/100) = 0.83/10 = 0.911. Hence, the value of √0.83 = 0.911
visual curriculum