Pythagorean Triples

Pythagorean triples are any three positive integers that completely satisfy the Pythagorean theorem. The theorem states that in any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two legs of the right triangle. These three sides of the right triangle form the Pythagorean triples. Let us learn how to generate a few Pythagorean triples in this article.

1.	What are Pythagorean Triples?
2.	Examples of Pythagorean Triples
3.	Pythagorean Triples Proof
4.	List of Pythagorean Triples
5.	FAQs on Pythagorean Triples

Pythagorean triples are a set of 3 positive numbers that fit in the formula of the Pythagoras theorem which is expressed as, a² + b² = c², where a, b, and c are positive integers. Here, 'c' is the 'hypotenuse' or the longest side of the triangle and 'a' and 'b' are the other two legs of the right-angled triangle. The Pythagorean triples are represented as (a,b, c). The most popular example of Pythagorean triples is (3, 4, 5). We can verify that 3, 4 and 5 satisfy the equation a² + b² = c². Let us see how! 3² + 4² = 5² ⇒ 9 + 16 = 25. Observe the right-angled triangle given below which shows the Pythagorean triples, 3, 4, and 5.

The set of the Pythagorean triples is endless. The first known Pythagorean triples is (3, 4, and 5). We can generate a few more triples by scaling them up in the following manner. We can create as many triples as possible by taking values for n.

n	(3n, 4n, 5n)
2	(6, 8, 10)
3	(9, 12, 15)
4	(12, 16, 20)

Let us consider Pythagorean triples (9, 40, 41) for which we can verify the Pythagorean formula (Hypotenuse² = side 1² + side 2²). The hypotenuse of the right-angled triangle is the longest side = 41

Hypotenuse² = 41² = 1681

The other two sides of the right angled triangle = 9 and 40

side 1² + side ² ⇒ 9² + 40² ⇒ 81 + 1600 = 1681

Thus, for any 3 Pythagorean Triples, we can verify the Pythagorean formula.

Tips and Tricks

• If we know one of the 3 triples, we can find the other two. If the given number (n) is an odd number, the Pythagorean triples are of the form, (n, (n²/2 - 0.5) and (n²/2 + 0.5)). For example, consider 5. The triples are (5, 25/2 - 0.5, 25/2 + 0.5) Finally, we get (5, 12 and 13)
• If the given number (n) is an even number, the Pythagorean triples are of the form = n, (n/2)²-1), ((n/2)²+1). For example, consider 6. The triples are (6, (3)² - 1, (3)² + 1) Finally, we get (6, 8, and 10)

The following table shows a list of a few Pythagorean Triples.

(3, 4, 5)	(5,12,13)	(7, 24, 25)
(8, 15, 17)	(9, 40, 41)	(11, 60, 61)
(12,35, 37)	(13, 84, 85)	(15, 112, 113)
(16, 63, 65)	(17,144, 145)	(19, 180, 181)
(20, 21, 29)	(20, 99 ,101)	(21, 220,221)

How to Generate Pythagorean Triples?

In order to generate Pythagorean triples, we use a formula, which is also known as the Pythagorean triple checker. Observe the figure given below and make the following assumptions where:

• a, b = legs of a right-angled triangle
• c = Hypotenuse of the right-angled triangle
• m, n are any two positive integers; and where m > n
• m and n are coprime numbers and both should not be odd numbers.

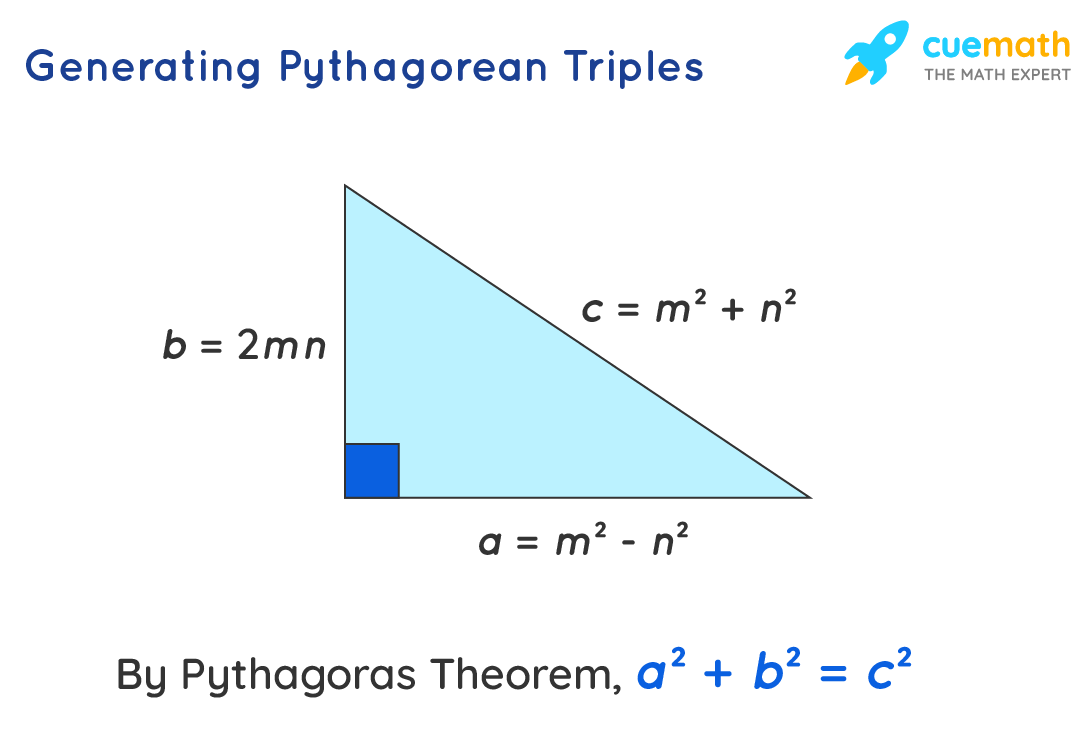
Let us assume any 2 integers 'm' and 'n', which will help us in generating the Pythagorean formula. Now, the lengths of our sides are a, b, and c. We will use 'm' and 'n' in order to find the exact values of the sides.

• The length of side 'a' is determined by defining the difference between the squares of 'm' and 'n' which is expressed as a = m² - n²
• The length of side 'b' is determined by doubling the product of 'm' and 'n'. This makes it b = 2mn in the equation form.
• Finally, the length of side 'c' is computed by the sum of the squares of m and n. This can be expressed as c = m² + n²

Now, we have concluded the following formulas:

• a = m²- n²
• b = 2mn
• c = m²+ n²

It is to be noted that any one of the formulas given above can be used based on the condition and the requirement of finding the Pythagorean triples. To generate random Pythagorean triples, consider random natural numbers m and n, such that m > n and determine the triples (a,b,c) such that a = m²- n², b = 2mn, c = m²+ n²

Example: Let us generate Pythagorean triples using the two integers 2 and 3.

Solution: Since m > n, m = 3, and n = 2. Now that we know the values of m and n, let us substitute those values into the formulas of a, b, and c, to get the sides of the right triangle.

Computing a:

a = m² - n²

a = 3² - 2²

9 - 4 = 5

a = 5

Computing b:

b = 2mn

b = 2 × 3 × 2

b = 12

Computing c:

c = m² + n²

c = 3² + 2²

c = 13
Let us see if our values for a = 5, b = 12, and c = 13 satisfy the Pythagorean theorem, which is a² + b² = c²

LHS: 5² + 12² = 25 +144 = 169

RHS : 13² = 169
Yes, it does! Therefore, (5, 12, 13) are Pythagorean triples.

Important notes

• Any three positive integers which satisfy the Pythagorean theorem formula of a² + b² = c² are known as Pythagorean triples.
• Pythagorean triples cannot be expressed in decimals.

☛ Related Articles

• Hypotenuse Leg Theroem
• Pythagorean Theorem Calculator
• Pythagorean Triples Calculator

 

What are Pythagorean Triples?

Pythagorean triples are the 3 positive integers that satisfy the Pythagoras theorem formula. This means if any 3 positive numbers are substituted in the Pythagorean formula c² = a² + b², and they satisfy the equation, then they are considered to be Pythagorean triples. Here, 'c' represents the longest side (hypotenuse) of the right-angled triangle, and 'a' and 'b' represent the other 2 legs of the triangle.

How to Find Pythagorean Triples?

In order to find whether a given set of numbers are Pythagorean triples or not, we substitute them in the Pythagoras theorem equation, and if they satisfy the equation, then they are considered to be Pythagorean triples. In some cases, if any one of the 3 numbers is given and we need to find the other two numbers we use the following method:

• If the given number is odd, then we calculate the other two numbers using: (n, (n²/2 - 0.5) and (n²/2 + 0.5)), where n = the given number.
• If the given number is even, then we calculate the other two numbers using: (n, (n/2)² - 1) and (n/2)² + 1)), where n = the given number.

What are the Pythagorean Triples of 6?

The Pythagorean triples for 6 are (6, 8, 10) as they satisfy the equation a² = b² + c². Since 6 is an even number, the other two numbers can be calculated using (n, (n/2)² - 1) and (n/2)² + 1)), where n = the given number. After substituting the value of n = 6, we get, (6, (6/2)² - 1) and (6/2)² +1)) = (6, (3)² - 1) and (3)² + 1)) = (6, 8 and 10).

Can Pythagorean Triples have Decimals?

Pythagorean triples are positive integers that satisfy the Pythagorean theorem. These are natural numbers that cannot be decimals.

What are the 5 Most Common Pythagorean Triples?

The 5 most common Pythagorean triples are (3, 4, 5), (5, 12, 13), (6, 8, 10), (9, 12, 15), and (15, 20, 25).

How to Find the Pythagorean Triples of 12?

In order to find the Pythagorean triples of 12, we will first check if the number is even or odd. Here, 12 is even. So the triples can be calculated using, (n, (n/2)² - 1) and (n/2)² + 1)), where n = the given number. Here, n = 12. Therefore, after substituting the value of n, we get, (12, (12/2)² - 1, (12/2)² + 1). Therefore, we have the Pythagorean triples of 12 as (12, 35, 37).

How to Find the Pythagorean Triples of 7?

In order to find the Pythagorean Triples of 7, we need to check if the number is even or odd. Here, 7 is an odd number, So the triples can be calculated using, (n, (n²/2 - 0.5) and (n²/2 + 0.5)), where n = the given number. Here, n = 7. Therefore, after substituting the values we get (7, (7² / 2 - 0.5), (7² / 2 - 0.5)). Therefore, we have the Pythagorean Triples of 7 as (7, 24, 25).