Semicircle
A semicircle is one of the most common shapes seen in geometry in the form of a protractor. A semicircle is half of a circle and some of the real-life examples that we see around us are a railway tunnel through which a train passes by, an igloo, half a watermelon, and much more. All these shapes resemble a semi-circle while drawn on a 2D plane.
| 1. | What is Semicircle? |
| 2. | Area of a Semicircle |
| 3. | Circumference of a Semicircle |
| 4. | Semicircle Perimeter |
| 5. | Angle Inscribed in a Semicircle |
| 6. | FAQs on Semicircle |
What is Semicircle?
If a circle is cut into half along the diameter, that half-circle is called a semicircle. The two halves are of equal measure. A semicircle can also be referred to as a half-disk and it represents a circular paper plate folded into halves. There is one line of symmetry in the semicircle that is considered as the reflection symmetry. Since the semicircle is the half of a circle which is 360°, hence the arc of the semicircle always measures 180°.
Definition of a Semicircle: When an arc of a circle with its endpoints on the diameter cuts a circle into two equal halves, those halves are called semicircles. It is the most common shape we find in real life, for example, the shape of the protractor, speedometer, taco, and so on. The image below represents a semicircle PQR along with the arc and the diameter (PQ) with both endpoints. Here, point J is the center, and PJ and JQ are the radii of the semicircle.
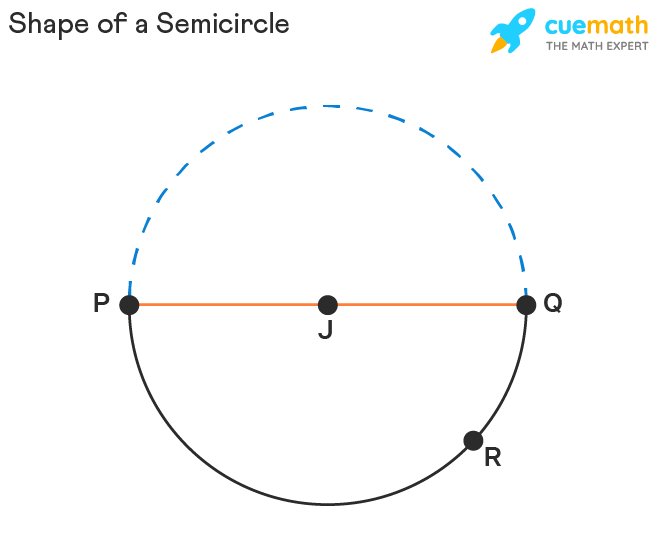
Now, let us look at some important properties of a semicircle.
Properties of Semicircle
Listed below are a few important properties of a semicircle that makes it a unique shape in geometry:
- A semicircle is a closed 2D shape.
- It is not a polygon since it has a curved edge.
- A semicircle has one curved edge which is its circumference and 1 straight edge which is called its diameter.
- It is exactly half of the circle. The diameter of the circle and the two semicircles formed out of it are the same.
- The area of a semicircle is half of the area of the circle.
Area of a Semicircle
The area of a circle refers to the region or inner space of the circle. Since we know that a semicircle is half a circle, the semicircle area will be half of the area of a circle. So, the area of a circle is πR2 where R is the radius of the circle. Hence,
Area of a Semicircle = πR2/ 2 square units
where,
Circumference of a Semicircle
The circumference of a semicircle is considered half of the circle's circumference. The circumference of a semicircle is defined as the measurement of the arc that forms a semicircle. It does not include the length of the diameter. As we know that the circumference of the circle formula is 2πR, where R is the radius. Therefore,
Circumference of a Semicircle = 2πR/2 = πR units
Semicircle Perimeter
The perimeter of a semicircle is the sum of its circumference and diameter. It is not similar to the area of the semicircle i.e. the perimeter is not the half perimeter of a circle. In fact, to calculate the perimeter of a semicircle we need to know either the diameter or radius of a circle along with the length of the arc. To determine the length of the arc, we need the circumference of a semicircle. Since the circumference is C = πR, where C is the circumference, and R is the radius, we can determine the formula for the perimeter of a semicircle which is:
The perimeter of a Semicircle = (πR + 2R) units, or after factoring the R, the perimeter of a semicircle = R(π + 2) units,
where,
- R is the radius of the semicircle
- π(pi) is 22/7 or 3.142 approximately
Angle Inscribed in a Semicircle
The inscribed angle is the angle formed by the line segments drawn from each end of the diameter to any point on the semicircle. No matter where the line touches the semicircle, the angle that is inscribed is always 90°. In the below image, we can see that angle B is at 90 degrees, and the diameter AC is 180°. Since a semicircle is half of a circle, the angle formed by the arc that makes the circle a semicircle measure 180°.

► Related Topics
Listed below are a few interesting topics that are related to semicircle shape in geometry, take a look!
Semicircle Examples
-
Example 1: Next to Dan's house is a garden in the shape of a circle with a diameter of 12 yards. Dan wants to use only half the garden for a party, what is the perimeter of the part he wants to use?
Solution: We know that the diameter = 12 yards, we need to find the radius.
Radius = Diameter/2 = 12/2 = 6 yards
So, the perimeter of a semicircle = R(π + 2) where π is 3.142 approx.
Perimeter = 6 (3.142 + 2)
Perimeter = 6 × 5.142
Perimeter = 30.852 yards
Therefore, the perimeter of half the garden that is going to be used by Dan is 30.852 yards.
-
Example 2: The radius of a circular cake is 7 units. Find the area of half of the cake.
Solution: We know that the radius = 7 units. The area of a semicircle = πR2/ 2 square units.
So, by substituting the value of the radius, Area = ((22/7) × 7 × 7)/2
Area = (22 × 7)/2
Area = 77 square units
Therefore, the area of half of the cake is 77 square units.
-
Example 3: Find the circumference of a semicircle with a diameter of 8 units.
Solution:
Given, diameter = 8 units.
So, radius = 8/2 = 4 units.
The formula to calculate the circumference of a semicircle is πR. Hence, by substituting the values of π and radius in this formula, we get,Circumference = 3.142 × 4 units
Circumference = 12.568 units
Therefore, the circumference of the given semicircle is 12.568 units approximately.

FAQs on Semicircle
What is the Definition of a Semicircle?
A semicircle is half of a circle. It is a 2D shape formed when a circle is cut into two equal parts. We can create two semi-circles from any circle. Some of the real-life examples of a semicircle are the shape of a protractor, the shape of a round paper folded in half, etc.
How to Find the Area of a Semicircle?
The area of a semicircle is the region within the boundary of the semicircle. It is the exact half of the area of a circle, which is πR2, where R is the length of the radius of the circle. Hence, the area of the semicircle = πR2/ 2 square units.
How to Find the Perimeter of a Semicircle?
The perimeter of a semicircle is not half of a full circle perimeter. Instead, the perimeter of a semicircle is the sum of the length of the arc and the diameter. Hence, the formula to calculate the perimeter of a semicircle is (πR + 2R) units, where R is the radius of the semicircle.
What is the Angle Inscribed in a Semicircle?
The angle inscribed in a semicircle is the angle formed by the segments drawn from both the ends of the diameter to any point on the semicircle. The angle inscribed in a semicircle is always 90° or a right angle.
Is Perimeter and Circumference of a Semicircle Similar?
When the circumference of a semicircle is the length of the arc which is half of the circle's circumference, i.e. 2πR/2 = πR, where R = radius of the semicircle, the perimeter of a semicircle is the sum of its circumference and diameter. It is the total length of the boundary including the diameter. It is calculated by the formula (πR + 2R) units.
What is the Diameter of a Semicircle?
Just like a circle, the diameter of a semicircle is twice the radius. If we form a semicircle by cutting a circle into two equal parts, then the diameter of the circle and the two semicircles formed is the same.
What is Half a Semicircle Called?
Half a semicircle is commonly called a quadrant. But since a semicircle can be cut into halves in many different ways, there is no specific term for those parts.
What is the Radius of a Semicircle?
The radius of the semicircle is the length of the segment drawn from its center to any point on its boundary. If a circle is cut to form two semicircles, then the radius of the semicircle is the same as the radius of the circle.
What is Semicircle in Circle?
A circle, when divided into two equal parts along with its diameter, forms two semicircles. So, in every circle, there are two semicircles the sum of whose areas is equal to the area of the circle.
What are the Semicircle Formulas Used in Geometry?
In geometry, the two main semicircle formulas that are used are:
- The formula to calculate the area of a semicircle with radius 'R' is given as πR2/ 2 square units.
- The formula to calculate the perimeter of a semicircle with radius 'R' is given as (πR + 2R) units.
visual curriculum