Area of Scalene Triangle
The total area of a scalene triangle is the area between the boundaries of the scalene triangle. A scalene triangle is a special type of triangle where all three sides of the triangle are of different lengths as well as the angles are of different measures. Although all the angles of a scalene triangle are different the sum of all the interior angles of the triangle is still 180 degrees. We will discuss the area of the scalene triangle, the formula for calculating the area along with the solved examples, and a few practice questions in the end.
| 1. | What is the Area of a Scalene Triangle? |
| 2. | Area of a Scalene Triangle Formula |
| 3. | Calculation of Area |
| 4. | List of Area of Scalene Triangle Formula |
| 5. | FAQs on Area of Scalene Triangle |
What is the Area of Scalene Triangle?
The area of a scalene triangle can be defined as the amount of space covered by a flat surface inside the scalene triangle. It is measured as the "number of" square units (square centimeters, square inches, square feet, etc.).

Area of a Scalene Triangle Formula
The formula of the area of the scalene triangle is used to find the area occupied by the scalene triangle within its boundary. The area of the scalene triangle is obtained by taking half of the product of the base to the height of the triangle. Thus, the formula for the area of the scalene triangle, with a base "b" and height "h" is "(1/2) bh".
Or, Area of a Scalene Triangle = [(1/2) × base × height] square units
Calculation of Area of a Scalene Triangle
As the triangle has 6 quantities namely 3 sides and 3 angles, the area of a triangle is calculated via various formulas depending upon the known quantities of the triangle.
-
Area of Scalene Triangle With Base and Height
When the base and height of the scalene triangle is known, then the area of a triangle is:
Area of a triangle = (1/2) × Base × Height
where b and h are the base and height of the triangle respectively.
-
Area of Scalene Triangle Using Heron's Formula
Heron's formula is applicable when all three sides of the triangle are known to us.
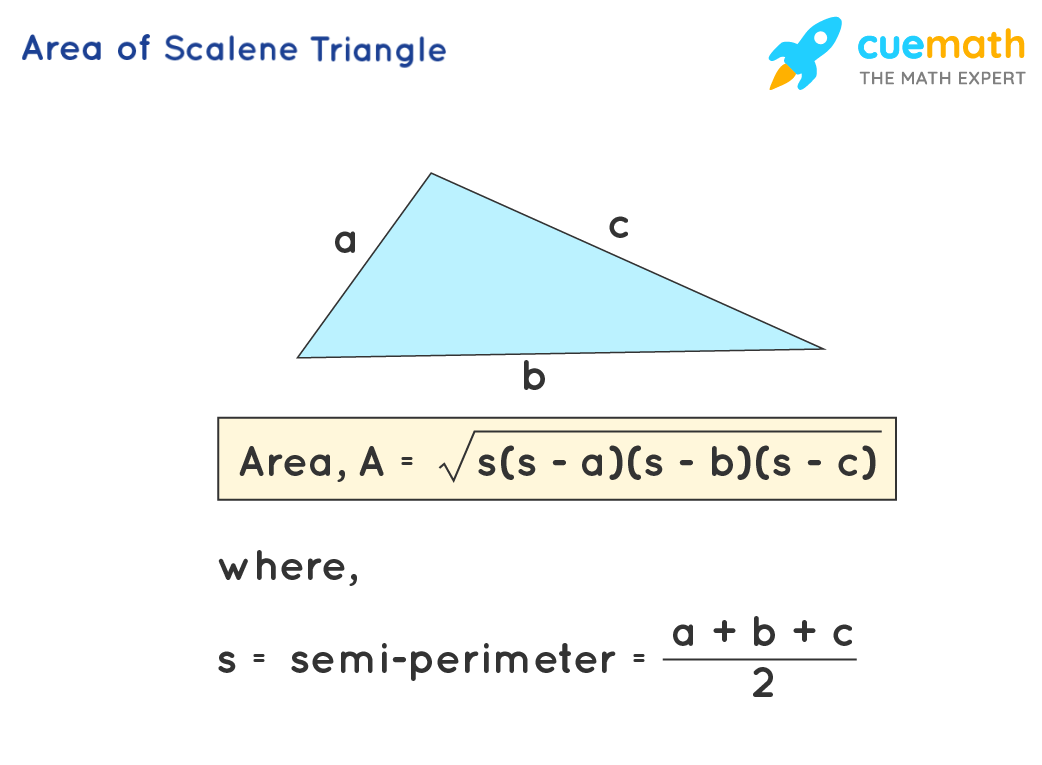
Consider the triangle ABC with sides a, b, and c has shown in the image.
Heron’s formula is: \(\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}\)
where, a, b, c are the side length of the triangle, and, s is the semi-perimeter and equals (a+b+c)/2.
-
Area of the Scalene Triangle With 2 Sides and Included Angle (SAS)
We can find the scalene triangle's area when the length of its two sides and the included angle are given.
1. When two sides b and c and included angle A is known, the area of the triangle is, Area = (1/2) bc × sin A
2. When sides a and c and included angle B is known, the area of the triangle is, Area = (1/2) ac × sin B
3. When sides a and b and included angle C is known, the area of the triangle is, Area = (1/2) ab × sin C
List of Area of Scalene Triangle Formula List
The area of a triangle can be calculated using the formulas discussed above. Here is a list of all those formulas:
| Area of the ScaleneTriangle When | Formula |
|---|---|
| Base and height of a triangle are given | (1/2) × base × height |
| Sides of a triangle are given | \(\sqrt {s(s - a)(s - b)(s - c)} \) where a, b, c are the sides and s is the semi-perimeter, s = (a + b + c)/2 |
| Two sides and the included angle are given | \(\dfrac{1}{2}\: {\text{side}_1} \times {\text{side}_2} \times \sinθ\) where 'θ' is the angle between the given two sides. |
Related Topics
Listed below are a few topics related to area of scalene triangle, take a look.
Area of a Scalene Triangle Formula Examples
-
Example 1: The height and base of a scalene triangle are 5 in and 8 in respectively. Find the area of the scalene triangle.
Solution:
Length of the base, b = 5 in
The height of the triangle is: h = 8 in
Area of the triangle = (1/2) × b × h
A = (1/2) × 5 × 8
⇒ A = 5 × 4
⇒ A = 20
Therefore, the area of the triangle is 20 square inches.
-
Example 2: Robert was given the two sides of the triangle and the corresponding angle between them as 14 units, 28 units, and 30 degrees respectively. Find the area of this triangle.
Solution:
The first side of the triangle, a = 14
The second side of the triangle, b = 28
The angle between the sides, C = 30 degrees
Using the area of the base is: Area (A) = (1/2) ab × sin C
A = (1/2) × 28 × 14 × sin 30º
⇒ A = (1/2) × 28 × 14 × (1/2)
⇒ A = 7 × 14
⇒ A = 98
So, The area of the given triangle is 98 squared units.

FAQs on Area of a Scalene Triangle Formula
What Is the Area of a Scalene Triangle and the Perimeter of the Scalene Triangle in Math?
The area of a figure is the region enclosed by the scalene triangle. The perimeter of a scalene triangle is the total length of the boundary of the figure.
What Is the Formula to Calculate Area of Scalene Triangle?
The area of the scalene triangle can be calculated using different formulas,
- Using base and height: (1/2) × base × height
- Using Heron's formula: \(\sqrt {s(s - a)(s - b)(s - c)} \), where where a, b, c are the sides and s is the semi-perimeter, s = (a + b + c)/2.
- Using Trigonometry: \(\dfrac{1}{2}\: {\text{side}_1} \times {\text{side}_2} \times \sinθ\), where 'θ' is the angle between the given two sides.
How Do You Find the Area of a Scalene Triangle?
The area of a triangle can be calculated by applying different formulas depending upon the known parameters.
- The area of the scalene triangle can be calculated using the base and height by finding half of the product of the base and the height of the scalene triangle.
- Given the measure of three sides of the scalene triangle, Heron's formula can be used to find the area of the scalene triangle, A \(\sqrt {s(s - a)(s - b)(s - c)} \), where a, b, c are the sides and s is the semi-perimeter, s = (a + b + c)/2.
- We can calculate the area of scalene triangle when the two sides and the included angle are given as, Area = \(\dfrac{1}{2}\: {\text{side}_1} \times {\text{side}_2} \times \sinθ\), where 'θ' is the angle between the given two sides.
How Do You Find the Area of a Scalene Triangle Without Height?
Heron's formula can be used to find the area of a triangle when the length of the 3 sides of the triangle is known. Hence, the area of the triangle can be calculated using Heron's formula without using height. The formula to calculate area in this case is given as, A = \(\sqrt {s(s - a)(s - b)(s - c)} \), where 's' is the semi-perimeter.
How Do You Find the Area of a Scalene Triangle Given Two Sides and an Angle?
The area of a triangle is half the product of the given two sides and sine of the included angle. For a detailed explanation refer to Area of Triangle with 2 Sides and Included Angle (SAS)
How Do You Find the Area of a Scalene Triangle With 3 Sides?
The area of a triangle with 3 sides can be calculated using Heron's formula, that is Area = \(\sqrt {s(s - a)(s - b)(s - c)} \), where 's' is the semi-perimeter, and 'a', 'b', and 'c' are the sides of scalene triangle.
How Do You Find the Area of an Irregular Scalene Triangle?
The area of an irregular triangle (sometimes referred to as a scalene triangle) can be calculated using the formula:\(\sqrt {s(s - a)(s - b)(s - c)} \), where, 's' is the semi-perimeter, and 'a', 'b', and 'c' are the sides of scalene triangle.
What Is the Height of a Scalene Triangle?
The height of a scalene triangle is the length of the perpendicular from one side of the triangle to the opposite vertex.
How Do You Calculate the Area of an Obtuse Triangle?
The area of an obtuse triangle can be calculated using the formula: (1/2) × base × height, by determining the length of any of its sides and height.
visual curriculum