CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC ~ ∆FEG, show that:
(i) CD/GH = AC/FG
(ii) ∆DCB ~ ∆HGE
(iii) ∆DCA ~ ∆HGF
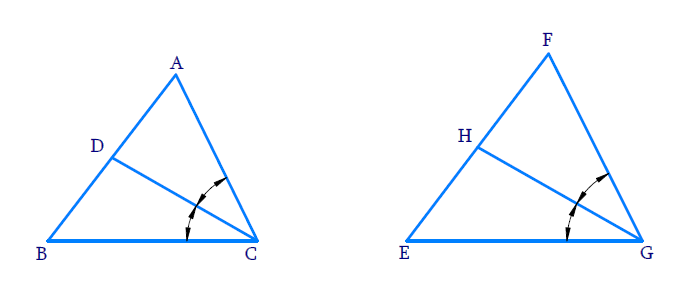
Solution:
(i) If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
This is referred to as the AA similarity criterion for two triangles.
∠ACB = ∠FGE (Given that ∆ABC ~ ∆FEG)
⇒ ∠ACB/2 = ∠FGE/2
⇒ ∠ACD = ∠FGH (CD and GH are bisectors of ∠C and ∠G respectively) ------------ (1)
In ∆ADC and ∆FHG
∠DAC = ∠HFG [∆ADC ~ ∆FEG]
∠ACD = ∠FGH [From equation (1)]
Thus, ∆ADC ~ ∆FHG (AA criterion)
⇒ CD/GH = AC/FG [If two triangles are similar, then their corresponding sides are in the same ratio]
(ii) If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
This is referred as AA similarity criterion for two triangles.
In ∆DCB and ∆HGE
∠DBC = ∠HEG [∆ABC ~ ∆FEG]
∠DCB = ∠HGE [∵ ∠ACB/2 = ∠FGE/2]
Thus, ∆DCB ~ ∆HGE (AA criterion)
(iii) If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
This is referred as AA similarity criterion for two triangles.
In ∆DCA and ∆HGF
∠DAC = ∠HFG [∆ABC ~ ∆FEG]
∠ACD = ∠FGH [∵ ∠ACB = ∠FGE]
Thus, ∆DCA ~ ∆HGF (AA criterion)
☛ Check: NCERT Solutions for Class 10 Maths Chapter 6
Video Solution:
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC ~ ∆FEG, show that: (i) CD/GH = AC/FG (ii) ∆DCB ~ ∆HGE (iii) ∆DCA ~ ∆HGF
NCERT Class 10 Maths Solutions Chapter 6 Exercise 6.3 Question 10
Summary:
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC ~ ∆FEG we have proved that CD/GH = AC/FG, ∆DCB ~ ∆HGE and ∆DCA ~ ∆HGF.
☛ Related Questions:
- In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥AC, prove that ∆ ABD ~ ∆ ECF.
- Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆ PQR (see Fig. 6.41). Show that ∆ ABC ~ ∆ PQR.
- D is a point on the side BC of a triangle ABC such that ∠ADC = ∠ BAC. Show that CA^2 = CB.CD.
- Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆ PQR.
visual curriculum