Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆ PQR
Solution:
We know if one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
This is referred as SAS criterion for two triangles.
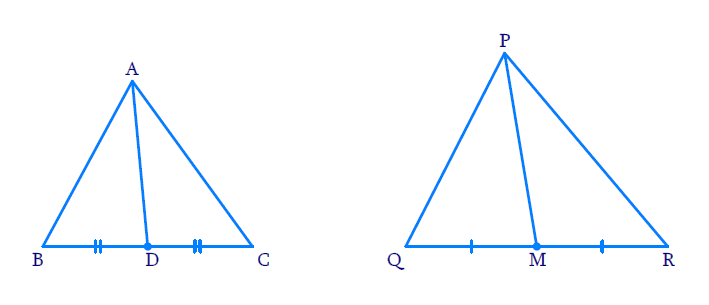

Produce AD to E so that AD = DE. Join CE
Similarly, produce PM to N such that PM = MN , and join RN.
In ΔABD and ΔCDE
AD = DE [By Construction]
BD = DC [AD is the median]
∠ADB = ∠CDE [Vertically opposite angles]
Therefore, ΔABD ≅ ΔECD [By SAS criterion of congruence]
⇒ AB = CE [CPCT] ...(i)
Also, in ΔPQM and ΔMNR
PM = MN [By Construction]
QM = MR [PM is the median]
∠PMQ = ∠NMR [Vertically opposite angles]
Therefore, ΔPQM = ΔNRM [By SAS criterion of congruence]
⇒ PQ = RN [CPCT]...(ii)
Now,
AB / PQ = AC / PR = AD / PM [Given]
⇒ CE / RN = AC / PR = AD / PM [from (i) and (ii)]
⇒ CE / RN = AC / PR = 2AD / 2PM
⇒ CE / RN = AC / PR = AE / PN [ 2AD = AE and 2PM = PN ]
Therefore, ΔACE ~ ΔPRN [By SSS similarity criterion]
Therefore, ∠CAE = ∠RPN
Similarly, ∠BAE = ∠QPN
Hence, ∠CAE + ∠BAE = ∠RPN + ∠QPN
⇒ ∠BAC = ∠QPR
⇒ ∠A = ∠P ....(iii)
Now, In ΔABC and ΔPQR
AB/PQ = AC/PR
∠A = ∠P [from (iii)]
Therefore, ΔABC ~ ΔPQR [By SAS similarity criterion]
☛ Check: NCERT Solutions Class 10 Maths Chapter 6
Video Solution:
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR
NCERT Class 10 Maths Chapter 6 Exercise 6.3 Question 14
Summary:
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Hence proved that ΔABC~ ΔPQR.
☛ Related Questions:
- In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that: (i) ΔABC ~ ΔAMP (ii) CA/PA = BC/MP.
- CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC ~ ∆FEG, show that: (i) CD/GH =AC/FG (ii) ∆DCB ~ ∆HGE (iii) ∆DCA ~ ∆HGF
- In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥AC, prove that ∆ ABD ~ ∆ ECF.
- Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆ PQR (see Fig. 6.41). Show that ∆ ABC ~ ∆ PQR.
visual curriculum