Expanded Form
The expanded form helps us to better understand a given number in maths. Let us take an example of the number 875294831. It is difficult to understand this number. Here an expanded form helps us to understand each of the digits based on their place value. Let us take a simple number 324 and try to find its expanded form. 324 is written in expanded form as 300 + 20 + 4. It means there are three hundred, two tens, and 4 ones in this number. We can easily understand the meaning of each digit of a number through its expanded form.
Trying to learn a number with a higher number of digits is very difficult without knowing how to express it in expanded form. The expanded form helps us to know the building blocks of higher numbers. Each of the digits can be written in the multiple forms of 1, 10, 100, 1000. Now with this understanding, let us move ahead to know more about the expanded form.
| 1. | What is the Meaning of Expanded Form? |
| 2. | Writing numbers in Expanded Form |
| 3. | Decimals in Expanded Form |
| 4. | FAQs on Expanded Form |
What is the Meaning of Expanded Form?
The way the whole numbers are formed well defines the number. The value of each digit in mathematics can be written in expanded form. Showing the number as a sum of each digit multiplied by its place value is the expanded form of a number. Let us look at the example of expanded form 1,278 = 1,000 + 200 + 70 + 8.
Expanded Form Definition
Expanded form is useful to split and present the higher digit number in its units, tens, hundreds, thousands form. An expanded form helps to better understand and rightly read the higher digit numbers. A number of the form 10030, is sometimes difficult to understand directly and can be represented in expanded form as 10030 = 10,000 + 30.
Some more examples of the expanded form are provided in the following table.
| Number | Ten Thousand | Thousands | Hundreds | Tens | Ones |
|---|---|---|---|---|---|
| 452 | 4 | 5 | 2 | ||
| 605 | 6 | 0 | 5 | ||
| 3854 | 3 | 8 | 5 | 4 | |
| 40980 | 4 | 0 | 9 | 8 | 0 |
Writing Numbers in Expanded Form
The expansion of a number is the separation of numbers based on place values. This is the intermediate step that helps us understand how the number has to be read. The expanded form helps us to know the place value of each digit within a number. Further, there are three different ways to write numbers in expanded form. The number 4537 can be written in one way of expanded form as 4531 = 4000 + 500 + 30 + 7, in the second way as 4531 = 4 × 1000 + 5 × 100 + 3 × 10 + 7 × 1, and in the third way as 4537 = 4 × thousands + 5 × hundreds + 3 × tens + 7 × ones.
Expanded Form in Maths: Here are the below steps, which you can follow to write the expanded form:
- Get the number in its standard form.
- Determine its place values using the place value chart.
- Multiply the number by its place value.
- Show it as, digit × place value.
- Represent all the digits as the product of the digit and its place value.
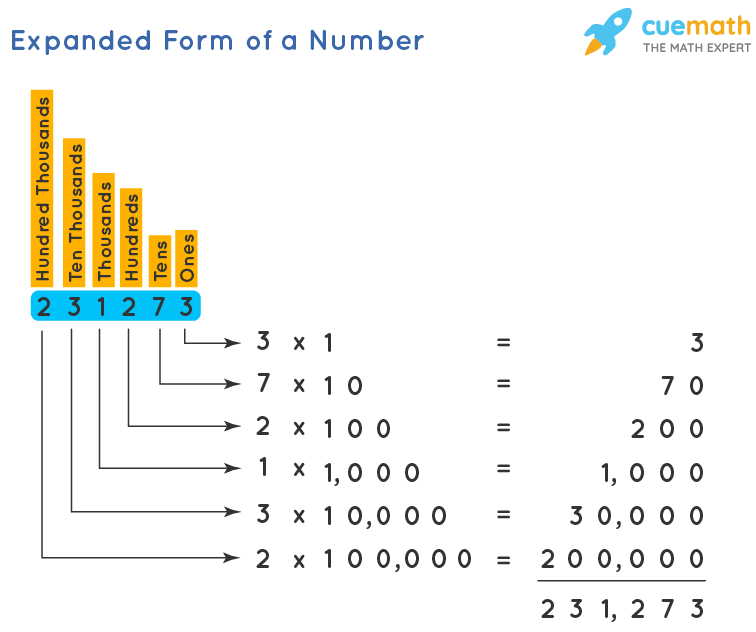
Any number we get to read is decomposed. This process is called expanding the number. After decomposing in the expanded form we interpret the number in its standard form. The following points help us to understand more about expanded form.
- Determine the place values of the digits for which the number is to be expanded.
- We decompose the number while we are expanding. i.e. breaking it according to its place values. For example, 431 = 400 + 30 + 1
- Expanded form in Maths helps us to understand how the number is formed using the place values.
Decimals in Expanded Form
Unlike whole numbers, decimal numbers can also be written in the expanded form. For writing the decimals in expanded form, we multiply each of the decimal digits with increasing exponent values of (1/10). Let us try to understand this with the help of a simple example of a decimal number. The decimal number 0.437 can be written in expanded form as 4 × (1/10) + 3 × (1/10)2 + 7 × (1/10)3= 4 × (1/10) + 3 × (1/100) + 7 × (1/1000) = 0.4 + 0.03 + 0.007
Now with the possibility of expressing decimals in expanded form, we can write any number in expanded form. A fraction, a percentage value can be converted into a decimal and the same can be written in the expanded form. A fraction of 1/7 in the decimal form would be 0.1428, 0.1428 in the expanded form would be 0.1428 = 1 × (1/10) + 4 × (1/10)2 + 2(1/10)3 + 8(1/10)4. And a percentage of 25% would be 0.25 = 2 × (1/10) + 5 × (1/10)2
☛Related Topics
Given below is the list of topics that are closely connected to the expanded form. These topics will also give you a glimpse of how such concepts are covered in Cuemath.
FAQs on Expanded Form
How to Multiply Using Expanded Form?
For the multiplication of expanded form, we need to first write the numbers in the expanded form and then multiply each of the constituents and then add back the numbers. Let us understand this with the help of the product of two numbers. 423 × 12 = (400 + 20 + 3) × (10 + 2) = 400 × 10 + 20 × 10 + 3 × 10 + 400 × 2 + 20 × 2 + 3 × 2 = 4000 + 200 + 30 + 800 + 40 + 6 = 4000 + (200 + 800) + (30 + 40) + 6 = 4000 + 1000 + 70 + 6 = 5000 + 70 + 6 = 5076.
How to Add Using Expanded Form?
For the addition of the expanded form, the individual numbers have to be written in expanded form and the addition of similar terms gives the final added answer. Let us understand this by adding two numbers 4896 + 3284 = (4000 + 800 + 90 + 6) + (3000 + 200 + 80 + 4) = (4000 + 3000) + (800 + 20) + (90 + 80) + (6 + 4) = 7000 + 1000 + 170 + 10 = 8000 + 170 + 10 = 8180.
What Is Expanded Form with Example?
An expanded form is to split a number and write in its thousands, hundreds, tens, and units form. An expanded form is helpful to know the place value of each of the digits. To understand the expanded form, let us check with a simple form of writing the expanded form of the number 6809. Here we write 6859 = 6000 + 800 + 50 + 9 and it means 6 thousands, 8 hundreds, 5 tens and 9 units.
What Is Expanded Form in Decimals?
The expanded form of expression is also possible for a decimal number. For a decimal number, each of the decimal digits is written as an exponent of one-tenth. The decimal 0.436 can be written in expanded form as 0.436 = 4 × (1/10) + 3 × (1/10)2 + 6 ×(1/10)3 = 4 × (1/10) + 3 × (1/100) + 6 ×(1/1000) = 0.4 + 0.03 + 0.006.
What Is the Difference Between Expanded Form and Standard Form?
The standard form is the combination of digits written together as a single number. In the expanded form the digits of the number are split into each of the individual digits with their place value and written in expanded form. The example of standard form of a number is 4,982 and the same number can be written in expanded form as 4 × 1000 + 9 × 100 + 8 × 10 + 2 × 1 = 4000 + 900 + 80 + 2.
Why Do We Need Expanded Form?
We need an expanded form to understand the given number better. The value of each digit based on its place value can be understood from the expanded form. In the beginning stage of learning numbers, the expanded form is very useful for knowing better about each of the digits within the number.
Can we Write an Expanded Form for Multiples of 10?
The expanded form can be written for multiples of 10 such as 40, 320, 700. The expanded for for these numbers are 40 = 4 × 10 + 0 × 1 = 40 + 0, 320 = 3 × 100 + 2 × 10 + 0 × 1 = 300 + 20 + 0, 700 = 7 × 100 + 0 × 10 + 0 × 1 = 700.
How Do You Write a Number in Expanded Form?
A number can be expressed in the expanded form by using the following steps:
- Determine each number's place values using the place value chart.
- Multiply the number by its place value.
- Show it as, digit × place value.
- Represent all the digits as the product of the digit and its place value.
How Do You Write 400 in Expanded Form?
The expanded form of 400 is written as 4 × 100 = 400.
How Do You Convert to Expanded Form?
Any number to be written in the expanded form first needs to be identified by its place value. Each number is multiplied by a corresponding multiple of 10 and add them. Conversion of numbers in expanded form to normal form is done by placing each digit in the proper places.