Harmonic Progression
Harmonic progression is obtained by taking the reciprocal of the terms of an arithmetic progression. The terms of a harmonic progression is of the form, 1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), 1/(a + 4d),...1/(a + (n - 1)d). Similar to the arithmetic progression, we can compute the nth term, the sum of n terms of the harmonic progression.
The concept of harmonic progression and harmonic mean has wide applications in math, physics, business, and other areas. Let us check the definition, formulas, examples, applications of harmonic progression.
| 1. | What Is Harmonic Progression? |
| 2. | Harmonic Progression Formulas |
| 3. | Applications of Harmonic Sequence |
| 4. | Examples on Harmonic Progression |
| 5. | Practice Questions |
| 6. | FAQs on Harmonic Progression |
What is Harmonic Progression?
The harmonic progression is formed by taking the reciprocal of the terms of the arithmetic progression. If the given terms of the arithmetic progression are a, a + d, a + 2d, a + 3d, ...., then the terms of the harmonic progression (or harmonic sequence) are 1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), 1/(a + 4d),...... Here a is the first term and d is a common difference. Both a and d have non-zero values.
The harmonic progression is an infinite series.
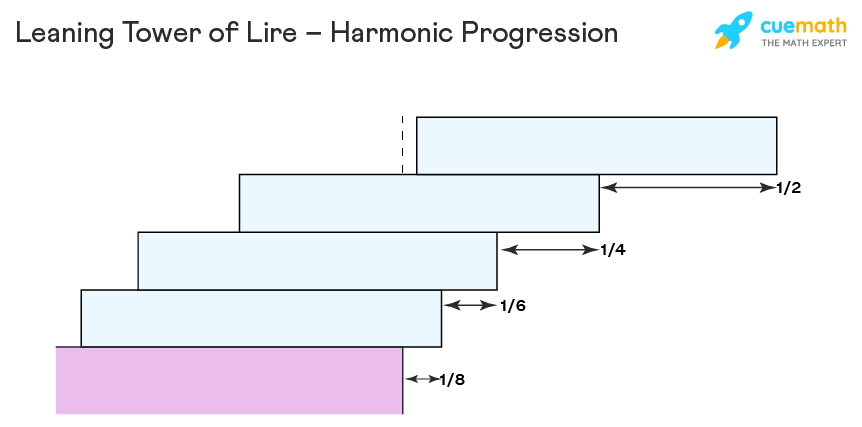
Leaning Tower of Lire: A good example of harmonic progression is the leaning tower of lire. Here a set of uniform sides blocks are stacked one over the other to achieve maximum sideways or lateral distance. The blocks have been stacked one-way distances of 1/2, 1/4, 1/6, 1/8, 1/16 ...... one over the other. The aim of this stacked arrangement is to achieve maximum sideway distances, such that the center of gravity is maintained and it does not collapse.
Harmonic Progression Formulas
The following formulas are helpful for numerous calculations involving harmonic progression.
nth term of a Harmonic Progression: It is the reciprocal of the nth term of the arithmetic progression. The nth term of the harmonic progression is the reciprocal of the sum of the first term and the (n - 1) times of the common difference. The nth term is useful to find any of the terms of the harmonic sequence.
nth Term of HP = 1/(a + (n - 1)d)
Harmonic Mean: In a harmonic progression, any term of the series is the harmonic mean of its neighboring terms.
Harmonic Mean = n /[1/a + 1/(a + d)+ 1/(a + 2d) +1/(a + 3d) +….]
- Harmonic mean of two terms a and b = (2ab) / (a + b).
- Harmonic mean of three terms a, b, and c = (3abc) / (ab + bc + ca).
- Sum of n terms of harmonic sequence = \(\dfrac{1}{d}.log \left(\dfrac{2a + (2n - 1)d}{2a - d}\right)\)
Relationship Between AM, GM, HM: Here is the relation between AM, GM, and HM for the given set of the arithmetic mean (AM), geometric mean (GM), harmonic mean(HM), the arithmetic mean is greater, followed by the geometric mean, and the harmonic mean.
AM > GM > HM
The square of the geometric mean is equal to the product of the arithmetic mean and harmonic mean.
GM2 = AM x HM
Application of Harmonic Sequence
Harmonic sequence and harmonic mean have numerous applications in other areas of mth, engineering, physics, and business. The following are some of the important applications of harmonic series.
- The average speed of a vehicle across two sets of equal distances can be computed using the harmonic mean of the respective speeds. If the speed of the vehicle is x mph for the first d miles and it is y mph for the next d miles, then the average speed of the vehicle across the entire distance is equal to the harmonic mean of these two speeds. Average Speed = (2xy) / (x + y).
- The density of a mix of substances or the density of the alloy of two or more substances of equal weight and equal weight percentage composition can be computed using the harmonic mean of the densities of the individual components.
- The focal length of a lens is equal to the harmonic mean of the distance of the object(u) from the lengs, and the distance of the image(v) from the lens. 1/f = 1/u + 1/v.
- In geometry, the radius of the incircle of a triangle is equal to one-third of the harmonic mean of the altitudes of the triangle.
- In the field of finance, the profit earning ratio is computed using the concept of the weighted harmonic mean of individual components.
☛Related Topics
The following topics would help in a better understanding of harmonic sequence.
Examples on Harmonic Progression
-
Example 1: Determine whether the following sequence is harmonic: -1, 1/2, -1/3, 1/4, -1/5, ....
Solution:
Let us take the reciprocals of the given sequence. Then we get -1, 2, -3, 4, -5, ...
Let us check whether this is an arithmetic progression by computing the common differences.
2 - (-1) = 3
-3 - 2 = -5
4 - (-3) = 7The differences are NOT the same and hence the given sequence is NOT harmonic.
Answer:The given sequence is NOT a harmonic sequence.
-
Example 2: What is the value of the 21st term and the nth term of the harmonic progression: 1/5, 1/9, 1/13, 1/14 .....?
Solution:
The given harmonic sequence is 1/5, 1/9, 1/13, 1/14 ...........
Comparing this with 1/a, 1/(a + d), 1/(a + 2d),..., we get 1/a = 1/5, 1/(a + d) = 1/9.
a = 5, a + d = 9, or d = 4.
The 21st term = 1/(a + 20d) = 1/(5 + 20 x 4) = 1/(5 + 80) = 1/85.
The nth term = 1/(a + (n - 1)d) = 1/(5 + (n - 1)4) = 1/(5 + 4n - 4) = 1/(4n + 1)
Answer: Therefore, the 21st term is 1/85, and the nth term is 1/(4n + 1).
-
Example 3: Find the 12th term of the harmonic progression, if the fifth term is 1/16, and the eighth term is 1/25.
Solution:
The fifth term = 1/(a + 4d) = 1/16
The eight term = 1/(a + 7d) = 1/25
Comparing this we have a + 4d = 16, and a + 7d = 25.
Solving these above two expressions we have a = 4, and d = 3.
The 12th term of the harmonic progression = 1/(a + 11d) = 1/(4 + 11x3) = 1/(4 + 33) = 1/37.
Answer: Therefore, the 12th term of the harmonic progression is 1/37.

FAQs on Harmonic Progression
What is a Harmonic Sequence?
The harmonic sequence is formed by taking the reciprocal of the terms of the arithmetic progression. The terms of the harmonic progression are 1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), 1/(a + 4d),...... Here,
- a is the first term and
- d is a common difference.
Both a and d have non-zero values. The harmonic progression can be finite or infinite.
What is Harmonic Progression Formula?
The formula for harmonic progression is the formula to find the nth term of the harmonic progression. The nth term of the harmonic progression is 1/(a + (n - 1)d).
What Is an Example of Harmonic Progression?
An example of harmonic progression is 1/2, 1/5, 1/8, 1/11.....
What Is the Difference Between Geometric Progression and Harmonic Progression?
The geometric progression is obtained by multiplying each term with a constant term called the common ratio, to obtain the next term. The harmonic progression is the reciprocal of the arithmetic progression, and each term of the arithmetic progression is obtained by adding a constant value to the successive terms, called the common difference. The geometric progression having a common difference or 'r' is a, ar, ar2, ar3,..... And the harmonic progression obtained from the arithmetic progression with a common difference of 'd' is 1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), 1/(a + 4d),.....1/(a + (n - 1)d).
What Is the Difference Between Arithmetic Progression and Harmonic Progression?
The harmonic progression can be said to be derived from arithmetic progression. The reciprocal of the terms of the arithmetic progression gives the harmonic progression. If the terms of the arithmetic progression are a, a + d, a + 2d, a + 3d, .....a + (n - 1)d, then the terms of the harmonic progression would be 1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), 1/(a + 4d),.....1/(a + (n - 1)d).
How Do We Solve Harmonic Progression?
The harmonic progression is solved by taking its reciprocal to form the arithmetic progression. Further, we need to find the first term and the common difference to solve more. The harmonic progression can be solved to find the nth term or to find the sum of n terms of the progression.
visual curriculum