Inverse of 2x2 Matrix

Before going to see how to find the inverse of a 2x2 matrix, let us recall the meaning of inverse. In general, the inverse of a real number is a number which when multiplied by the given number results in the multiplicative identity, which is 1. In matrices, the inverse of a matrix A (which is denoted by A^-1) is a matrix which when multiplied by A gives the identity matrix, I. i.e., AA^-1 = A^-1A = I. But how to find the inverse of 2x2 matrix?

Let us see the formula for finding the inverse of 2x2 matrix along with some other ways of finding it. Here, we can also see some examples of finding the inverse of a 2x2 matrix.

The inverse of a 2x2 matrix, say A, is a matrix of the same order denoted by A^-1 such that AA^-1 = A^-1A = I, where I is the identity matrix of order 2x2. i.e., I = \(\left[\begin{array}{rr}1 & 0 \\ \\ 0 & 1 \end{array}\right]\). In general, the inverse of a matrix A is found using the formula (adj A)/(det A), where "adj A" is the "adjoint of A" and "det A" is the "determinant of A". But in case of a 2x2 matrix A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), we can find the inverse directly using the following formula.

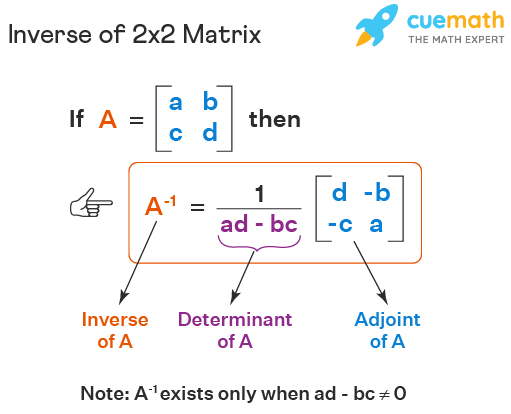
Note: Since ad - bc is in the denominator, it should NOT be 0 for A^-1 to be defined. i.e.,

• If ad - bc = 0, then A^-1 does NOT exist and in this case, we call A to be a singular matrix.
• If ad - bc ≠ 0, then A^-1 exists and in this case, we call A to be a non-singular matrix.

Let us see the process of finding the determinant and adjoint of a 2x2 matrix in detail here.

Determinant of a 2x2 Matrix

The inverse of a 2x2 matrix formula uses the determinant of the matrix. We know that the determinant of a 2x2 matrix A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\) is det(A) = ad - bc. i.e., to find the determinant, we just multiply the elements of each of the two diagonals and subtract (the product of principal diagonal's elements being the minuend).

Examples:

• The determinant of A = \(\left[\begin{array}{rr}3 & 2 \\ \\ 1 & 5 \end{array}\right]\) = (3 × 5) - (2 × 1) = 15 - 2 = 13.
• The determinant of B = \(\left[\begin{array}{rr}1 & -1 \\ \\ 0 & 2 \end{array}\right]\) = (1 × 2) - (-1 × 0) = 2 - 0 = 2.

Adjoint of a 2x2 Matrix

The adjoint of a matrix A is the transpose of the cofactor matrix of A. But for finding the adjoint of a 2x2 matrix, we don't need to have the headache of finding cofactors. There is a trick to find the adjoint of a 2x2 matrix. For a matrix A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), the adjoint is adj(A) = \(\left[\begin{array}{rr}d & -b \\ \\ -c & a \end{array}\right]\). i.e., to find the adjoint of a matrix,

• Interchange the elements of the principal diagonal.
• Just change (but do NOT interchange) the signs of the elements of the other diagonal.

Example: The adjoint of a matrix A = \(\left[\begin{array}{rr}3 & 2 \\ \\ 1 & 5 \end{array}\right]\) is adj A = \(\left[\begin{array}{rr}5 & -2 \\ \\ -1 & 3 \end{array}\right]\).

The inverse of any matrix A is found using the formula A^-1 = (adj A)/(det A). We already know how to find the adj A and det A for a 2x2 matrix. For any 2x2 matrix A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), adj A = \(\left[\begin{array}{rr}d & -b \\ \\ -c & a \end{array}\right]\) and det A = 1/(ad - bc). Substituting these values in the formula A^-1 = (adj A)/(det A),

• A^-1 = [1/(ad - bc)] \(\left[\begin{array}{rr}d & -b \\ \\ -c & a \end{array}\right]\)

Example: The inverse of a 2x2 matrix A = \(\left[\begin{array}{rr}3 & 2 \\ \\ 1 & 5 \end{array}\right]\) is,

A^-1 = [1/(3×5 - 2×1)] \(\left[\begin{array}{rr}5 & -2 \\ \\ -1 & 3 \end{array}\right]\)

= (1/13) \(\left[\begin{array}{rr}5 & -2 \\ \\ -1 & 3 \end{array}\right]\)

= \(\left[\begin{array}{rr}5/13 & -2/13 \\ \\ -1/13 & 3/13 \end{array}\right]\)

We already have seen the formula to find the inverse of 2x2 matrix. We can either use that formula or simply the following steps instead of the formula to find the inverse of 2x2 matrix. The steps are explained with an example where we are going to find the inverse of A = \(\left[\begin{array}{rr}1 & -1 \\ \\ 0 & 2 \end{array}\right]\).

• Step - 1: Find the det A just by cross multiplying the elements and subtracting. Note that the product of elements of principal diagonal should be done first.
  det A = (1 × 2) - (-1 × 0) = 2 - 0 = 2.
• Step - 2: Find adj A by interchanging the elements of the principal diagonal and changing the signs of the other diagonal.
  adj A = \(\left[\begin{array}{rr}2 & 1 \\ \\ 0 & 1 \end{array}\right]\).
• Step - 3: Find the inverse of A using the formula A^-1 = (adj A) / (det A). i.e., divide every element of adj A by det A.
  A^-1 = \(\left[\begin{array}{rr}2/2 & 1/2 \\ \\ 0/2 & 1/2 \end{array}\right]\) = \(\left[\begin{array}{rr}1 & 1/2 \\ \\ 0 & 1/2 \end{array}\right]\)

We can use the elementary row operations to find the inverse of a 2x2 matrix, A. The process is explained below with an example.

• We first write A and I (which is the identity matrix of order 2x2) as an augmented matrix separated by a line such that A is on the left side and I is on the right side.
• Apply row operations such that the left side matrix becomes the identity matrix I.
• Then the right side matrix is A^-1.

We can solve the system of equations using the inverse of a matrix. The steps to do the same are explained here with an example. Consider the system of 2x2 equations x + 2y = 5 and 3x - 5y = -7.

• Step - 1: Write the system in the form AX = B.
  \(\left[\begin{array}{rr}1 & 2 \\ \\ 3 & -5 \end{array}\right]\) \(\left[\begin{array}{rr}x \\ \\ y \end{array}\right]\) = \(\left[\begin{array}{rr}5 \\ \\ -7 \end{array}\right]\)
  Here, A = \(\left[\begin{array}{rr}1 & 2 \\ \\ 3 & -5 \end{array}\right]\), X = \(\left[\begin{array}{rr}x \\ \\ y \end{array}\right]\), and B = \(\left[\begin{array}{rr}5 \\ \\ -7 \end{array}\right]\).
• Step - 2: Find the inverse of the 2x2 matrix. i.e., find A^-1.
  A^-1 = [1/(1 × -5 - 2 × 3)] \(\left[\begin{array}{rr}-5 & -2 \\ \\ -3 & 1 \end{array}\right]\) = \(\left[\begin{array}{rr}5/11 & 2/11 \\ \\ 3/11 & -1/11 \end{array}\right]\)
• Step - 3: Find the solution matrix X using X = A^-1B.
  X = \(\left[\begin{array}{rr}5/11 & 2/11 \\ \\ 3/11 & -1/11 \end{array}\right]\) \(\left[\begin{array}{rr}5 \\ \\ -7 \end{array}\right]\)
  \(\left[\begin{array}{rr}x \\ \\ y \end{array}\right]\)= \(\left[\begin{array}{rr}(25/11)+(-14/11) \\ \\ (15/11+7/11) \end{array}\right]\)
  \(\left[\begin{array}{rr}x \\ \\ y \end{array}\right]\)= \(\left[\begin{array}{rr}1 \\ \\ 2 \end{array}\right]\)

Therefore, x = 1 and y = 2 is the solution of the given system of equations.

Important Points on Inverse of 2x2 Matrix:

Here are some important points about the inverse of a 2x2 matrix.

• A^-1 does not exist when det A = 0. i.e., a matrix is invertible only if det A ≠ 0.
• If A^-1 is the inverse of A, then AA^-1 = A^-1A = I.
• The inverse of an identity matrix is itself. i.e., I^-1 = I.
• A^-1 is used to solve a system of equations.

☛Related Topics:

• Matrix Multiplication
• Matrix Formula
• Inverse of 3x3 Matrix
• Inverse of 2x2 Matrix Calculator

What is the Inverse of a 2x2 Matrix?

The inverse of a 2x2 matrix A is denoted by A^-1 where AA^-1 = A^-1A = I. If A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), then A^-1 = [1/(ad - bc)] \(\left[\begin{array}{rr}d & -b \\ \\ -c & a \end{array}\right]\).

How to Find Inverse of a 2 by 2 Matrix?

To find the inverse of a 2x2 matrix A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\),

• Find det A = ad - bc.
• Find adj A = \(\left[\begin{array}{rr}d & -b \\ \\ -c & a \end{array}\right]\).
• Use the formula A^-1 = (adj A)/(det A).

What is an Example of a 2x2 Matrix with No Inverse?

A matrix has no inverse if its determinant is 0. A = \(\left[\begin{array}{rr}1 & 2 \\ \\2 & 4 \end{array}\right]\) is a matrix with no inverse as det A = (1 × 4) - (2 × 2) = 4 - 4 = 0.

What is the Trick / Shortcut to Find the Inverse of a 2x2 Matrix?

If A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), then adj A can be found just by interchanging the principal diagonal elements and changing the signs of the other diagonal elements. Also, det A = ad - bc. Then use A^-1 = (adj A) / (det A).

How to Find Inverse of 2x2 Matrix Using Adjoint?

If A is a 2x2 matrix, its inverse is A^-1 = (adj A)/(det A). If A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), then

• det A = ad - bc
• adj A = \(\left[\begin{array}{rr}d & -b \\ \\ -c & a \end{array}\right]\)
• A^-1 = (adj A)/(det A) = [1/(ad - bc)] \(\left[\begin{array}{rr}d & -b \\ \\ -c & a \end{array}\right]\)

How to Find Inverse of 2x2 Matrix Using Determinant?

The determinant of a 2x2 matrix \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\) is ad - bc. Its inverse is [1/(ad - bc)] \(\left[\begin{array}{rr}d & -b \\ \\ -c & a \end{array}\right]\).

Does a 2x2 Matrix have an Inverse?

A 2x2 matrix has inverse only if its determinant is non-zero. If it is zero, then the matrix has no inverse and in that case, it is called a singular matrix.

How to Find Inverse of a 2x2 Matrix Using Elementary Row Operations?

To find the inverse of a 2x2 matrix A using elementary row operations,

• Write A and I (identity matrix) in a single matrix separated by a line.
• Apply row operations to make the left side matrix to be I.
• The right side matrix is A^-1.