A day full of math games & activities. Find one near you.

Square Root of 240

The square root of 240 is expressed as √240 in the radical form and as (240)^½ or (240)^0.5 in the exponent form. The square root of 240 rounded up to 5 decimal places is 15.49193. It is the positive solution of the equation x² = 240. We can express the square root of 240 in its lowest radical form as 4 √15.

Square Root of 240: 15.491933384829668
Square Root of 240 in exponential form: (240)^½ or (240)^0.5
Square Root of 240 in radical form: √240 or 4 √15

1.	What Is the Square Root of 240?
2.	Is Square Root of 240 Rational or Irrational?
3.	Tips and Tricks
4.	How to Find the Square Root of 240?
5.	FAQs on Square Root of 240
6.	Challenging Questions

What Is the Square Root of 240?

The square root of 240 is the value which on multiplication with itself gives the final product as 240.

Is the Square Root of 240 Rational or Irrational?

We cannot find a whole number which on squaring gives 240. It is approximately written as a square of 15.4919, which is a non-recurring and non-terminating decimal number. This shows that 240 is not a perfect square and proves that the square root of 240 is an irrational number.

Tips and Tricks:

Square root of any non-perfect square number is always an irrational number. Hence, the square root of 240 is an irrational number.

How to Find the Square Root of 240?

The square root of 240 can be found using the long division method. The simplified radical form of the square root of 240 is given below.

Simplified Radical Form of Square Root of 240

240 can be written as a product of 3 and 80. It is given as:

√240 = √(3 × 80) = √( 2⁴ × 3 × 5) = 4√15

15 is not a perfect square. Hence, it stays within the root sign. However, 16 can be shown as 2⁴. Thus, the simplified radical form of the square root of 240 is 4√15.

Square Root of 240 by Long Division Method

The square root of 240 can be found using the long division method. These are the steps to be followed:

Step 1: Starting from the right, we will pair up the digits by putting a bar above them.
Step 2: Find a number such that when you multiply it with itself, the product is less than or equal to 240. Keeping the divisor as 25, we get the quotient as 15 and the remainder as 140-125 = 15.
Step 3: Double the divisor and enter it with a blank on its right. Then assume the largest digit to replace the blank. This will become the new digit in the quotient. Now, when the new divisor will be multiplied to the new quotient, the final product will be lesser than or equal to our dividend. Finally, divide and write the remainder. Guess the largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend. Divide and write the remainder. Repeat this process to get the decimal places you want.

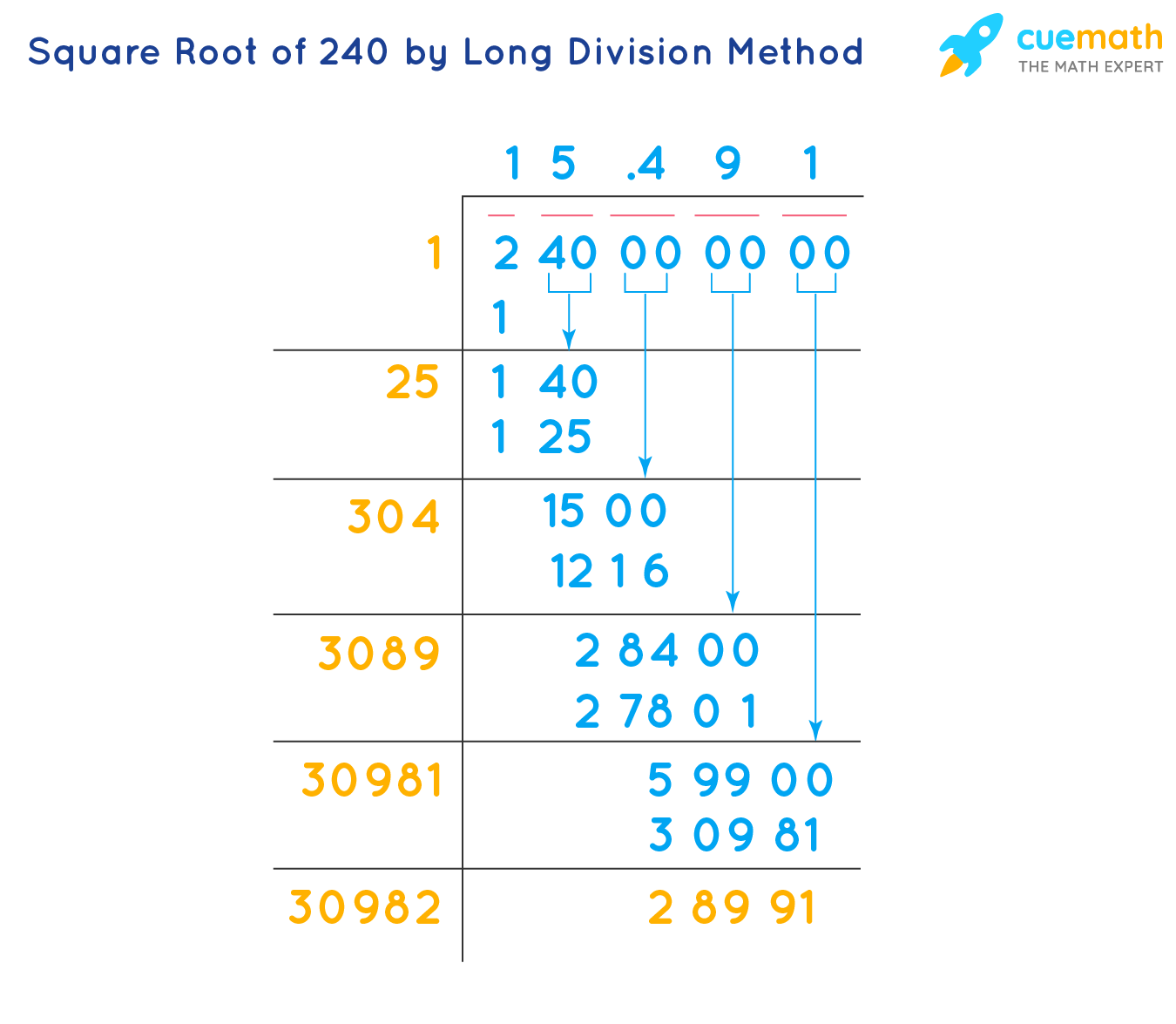
Thus, √240 = 15.491

Explore square roots using illustrations and interactive examples

Challenging Questions:

Find the square root of 240 using the long division method up to 8 decimal places.
How can you express the square root of 960 in terms of square root of 240?

Example 1: What are the two consecutive numbers between which the value of square root of 240 lies?

Solution

The perfect squares nearest to 240 are 225 and 256. The square root of 225 is 15. The square root of 256 is 16.
Hence, the two numbers between which the square root of 240 lies are 15 and 16.
Example 2: Evaluate (√240 - 2√15)/√240

Solution

As we know, √240 can be simplified as 4√15.
Hence, (√240 - 2√15)/√240 = (4√15 - 2√15)/4√15 = 2√15/4√15 = 1/2
Example: If the area of an equilateral triangle is 240√3 in². Find the length of one of the sides of the triangle.

Solution:

Let 'a' be the length of one of the sides of the equilateral triangle.
⇒ Area of the equilateral triangle = (√3/4)a² = 240√3 in²
⇒ a = ±√960 in
Since length can't be negative,
⇒ a = √960 = 2 √240
We know that the square root of 240 is 15.492.
⇒ a = 30.984 in

go to slide go to slide go to slide

Great learning in high school using simple cues

Indulging in rote learning, you are likely to forget concepts. With Cuemath, you will learn visually and be surprised by the outcomes.

Book a Free Trial Class

FAQs on the Square Root of 240

What is the Value of the Square Root of 240?

The square root of 240 is 15.49193.

Why is the Square Root of 240 an Irrational Number?

Upon prime factorizing 240 i.e. 2⁴ × 3¹ × 5¹, 3 is in odd power. Therefore, the square root of 240 is irrational.

Evaluate 20 plus 2 square root 240

The given expression is 20 + 2 √240. We know that the square root of 240 is 15.492. Therefore, 20 + 2 √240 = 20 + 2 × 15.492 = 20 + 30.984 = 50.984

What is the Square Root of 240 in Simplest Radical Form?

We need to express 240 as the product of its prime factors i.e. 240 = 2 × 2 × 2 × 2 × 3 × 5. Therefore, √240 = √2 × 2 × 2 × 2 × 3 × 5 = 4 √15. Thus, the square root of 240 in the lowest radical form is 4 √15.

What is the Value of 17 square root 240?

The square root of 240 is 15.492. Therefore, 17 √240 = 17 × 15.492 = 263.363.

If the Square Root of 240 is 15.492. Find the Value of the Square Root of 2.4.

Let us represent √2.4 in p/q form i.e. √(240/100) = 2.4/10 = 1.549. Hence, the value of √2.4 = 1.549

Math worksheets and
visual curriculum