Descriptive and Inferential Statistics
Descriptive and inferential statistics are two fields of statistics. Descriptive statistics is used to describe data and inferential statistics is used to make predictions. Descriptive and inferential statistics have different tools that can be used to draw conclusions about the data.
In descriptive and inferential statistics, the former uses tools such as central tendency, and dispersion while the latter makes use of hypothesis testing, regression analysis, and confidence intervals. In this article, we will learn more about descriptive and inferential statistics, its differences, associated formulas and examples.
What is Descriptive and Inferential Statistics?
The purpose of descriptive and inferential statistics is to analyze different types of data using different tools. Descriptive statistics helps to describe and organize known data using charts, bar graphs, etc., while inferential statistics aims at making inferences and generalizations about the population data.
Descriptive Statistics
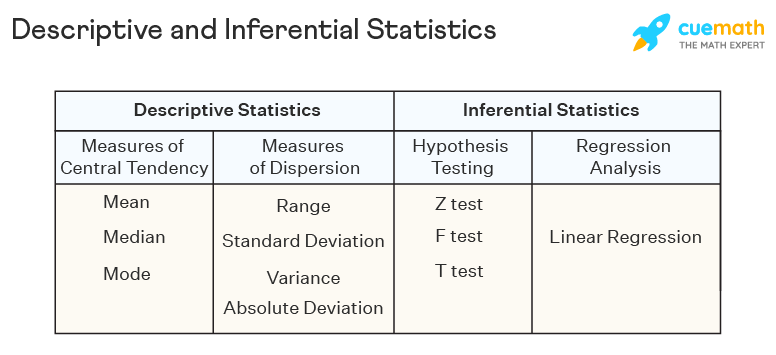
Descriptive statistics are a part of statistics that can be used to describe data. It is used to summarize the attributes of a sample in such a way that a pattern can be drawn from the group. It enables researchers to present data in a more meaningful way such that easy interpretations can be made. Descriptive statistics uses two tools to organize and describe data. These are given as follows:
- Measures of Central Tendency - These help to describe the central position of the data by using measures such as mean, median, and mode.
- Measures of Dispersion - These measures help to see how spread out the data is in a distribution with respect to a central point. Range, standard deviation, variance, quartiles, and absolute deviation are the measures of dispersion.
Inferential Statistics
Inferential statistics is a branch of statistics that is used to make inferences about the population by analyzing a sample. When the population data is very large it becomes difficult to use it. In such cases, certain samples are taken that are representative of the entire population. Inferential statistics draws conclusions regarding the population using these samples. Sampling strategies such as simple random sampling, cluster sampling, stratified sampling, and systematic sampling, need to be used in order to choose correct samples from the population. Some methodologies used in inferential statistics are as follows:
- Hypothesis Testing - This technique involves the use of hypothesis tests such as the z test, f test, t test, etc. to make inferences about the population data. It requires setting up the null hypothesis, alternative hypothesis, and testing the decision criteria.
- Regression Analysis - Such a technique is used to check the relationship between dependent and independent variables. The most commonly used type of regression is linear regression.
Difference Between Descriptive and Inferential Statistics
Both descriptive and inferential statistics are equally important to analyze data. Descriptive statistics are used to order data and describe the sample using the mean, standard deviation, charts, etc. Inferential statistics uses this sample data to predict the trend of the population data. The differences between descriptive and inferential statistics have been outlined in the table given below:
| Basis | Descriptive Statistics | Inferential Statistics |
|---|---|---|
| Definition | Descriptive statistics is used to describe the characteristics of the population using a sample. | Inferential statistics uses various analytical tools to draw inferences about the population using samples. |
| Tools | Measures of central tendency and measures of dispersion. | Hypothesis testing and regression analysis. |
| Use | Organizes, describes and presents data in a meaningful way with the help of charts and graphs. | Tests, predicts, and compares data obtained from various samples. |
| Relevance | It is used to summarize known data in a way that can be used for further predictions and analysis. | It tries to use the summarized samples to draw conclusions about the population. |
Descriptive and Inferential Statistics Formulas
There are many statistical formulas that fall under descriptive and inferential statistics. These are given as follows:
Descriptive Statistics:
- Mean = Σxi / n
- Mode = Most frequently occurring observation
- Median (n is odd) = [(n + 1) / 2]th term
- Median (n is even) = [(n / 2)th term + ((n / 2) + 1)th term] / 2
- Sample Variance = \(\sum \frac{\left ( X_{i}-\overline{X} \right )^{2}}{n - 1}\)
- Sample Standard Deviation = \(\sqrt{\sum \frac{\left ( X_{i}-\overline{X} \right )^{2}}{n - 1}}\)
- Range = Highest observation - Lower Observation.
Inferential Statistics
- Z score = \(\frac{x-\mu}{\sigma}\)
- F test statistic = \(\frac{\sigma_{1}^{2}}{\sigma_{2}^{2}}\)
Examples of Descriptive and Inferential Statistics
Descriptive and inferential statistics need to be used hand in hand so as to analyze the data in the best possible way. Some examples of descriptive and inferential statistics are given below:
- Suppose the scores of 100 students belonging to a specific country are available. The performance of these students needs to be examined. This data by itself will not yield any valuable results. However, by using descriptive statistics, the spread of the marks can be obtained thus, giving a clear idea regarding the performance of each student.
- Now suppose the scores of the students of an entire country need to be examined. Using a sample of, say 100 students, inferential statistics is used to make generalizations about the population.
Related Articles:
- Mean Median Mode
- Probability and Statistics
- Data Handling
- Summary Statistics
- Regression Coefficients
Important Notes on Descriptive and Inferential Statistics
- Descriptive and inferential statistics are used to analyze data, obtain samples and make inferences about the population.
- The tools used in descriptive statistics are measures of central tendency and dispersion.
- The tools used in inferential statistics are hypothesis testing and regression analysis.
Examples on Descriptive and Inferential Statistics
-
Example 1: The scores of 2 groups of students belonging to different classes are noted. Using descriptive and inferential statistics see which group exhibits a higher variability in performance.
Group A: 56, 58, 60, 62, 64
Group B: 40, 50, 60, 70, 80
Solution: To describe the variability in performance the variance is used. Thus, descriptive statistics is used to analyze this data.
Group A mean = (56 + 58 + 60 + 62 + 64) / 5 = 60
Group A variance = ([56 - 60)2 + (58 - 60)2 + (60 - 60)2 + (62 - 60)2 + (64 - 60)2] / 5 - 1 = 10
Group B mean = (40 + 50 + 60 + 70 + 80) / 5 = 60
Group B variance = ([40 - 60)2 + (50 - 60)2 + (60 - 60)2 + (70 - 60)2 + (80 - 60)2] / 5 - 1 = 250
By looking at the variance it is clear that group B displays higher variance than group A
Answer: Group B is more variable.
-
Example 2: Find the mode of the following data using descriptive statistics.
5, 6, 2, 7, 6, 5,1, 9, 5, 8, 5, 4, 3, 12, 11, 17, 5, 5Solution: Mode is the most frequently occurring observation. Thus, the mode is 5
Answer: Mode = 5
-
Example 3: Find the z score using descriptive and inferential statistics for the given data. Population mean 100, sample mean 120, population variance 49 and size 10.
Solution: Inferential statistics is used to find the z score of the data. The formula is given as follows:
z = \(\frac{x-\mu}{\sigma}\)
Standard deviation = \(\sqrt{49}\) = 7
z = (120 - 100) / 7
= 20 / 7 = 2.86
Answer: Z score = 2.86

FAQs on Descriptive and Inferential Statistics
What is the Meaning of Descriptive and Inferential Statistics?
Descriptive and inferential statistics are two branches of statistics that are used to describe data and make important inferences about the population using samples.
What are the Tools Used in Descriptive and Inferential Statistics?
The tools used in descriptive and inferential statistics are measures of central tendency, measures of dispersion, hypothesis testing, and regression analysis.
What are the Important Formulas in Descriptive and Inferential Statistics?
The important formulas used in descriptive and inferential statistics are as follows:
- Mean = Σxi / n
- Mode = Most frequently occurring observation
- Sample Variance = \(\sum \frac{\left ( X_{i}-\overline{X} \right )^{2}}{n - 1}\)
- F test statistic = \(\frac{\sigma_{1}^{2}}{\sigma_{2}^{2}}\)
When Do You Use Descriptive and Inferential Statistics?
Descriptive and inferential statistics are used to analyze data. Descriptive statistics is used to describe and organize data while inferential statistics draw conclusions about the population from samples by using analytical tools.
Is Hypothesis Testing a Part of Descriptive and Inferential Statistics?
Yes, hypothesis tests such as z test, f test, ANOVA test, and t-test are a part of descriptive and inferential statistics. Hypothesis testing along with regression analysis specifically fall under inferential statistics.
What Is the Similarity Between Descriptive and Inferential Statistics?
The similarity between descriptive and inferential statistics is that they both rely on the same data set. Descriptive statistics describes this data set while inferential statistics uses this data set to make generalizations about a population
What is the Difference Between Descriptive and Inferential Statistics?
The main difference between descriptive and inferential statistics is that the former is used to describe the characteristics of a data set while the latter focuses on making predictions and generalizations about the data.
visual curriculum