Exponential Function
The exponential function is a type of mathematical function which are helpful in finding the growth or decay of population, money, price, etc that are growing or decay exponentially. Jonathan was reading a news article on the latest research made on bacterial growth. He read that an experiment was conducted with one bacterium. After the first hour, the bacterium doubled itself and was two in number. After the second hour, the number was four. At every hour the number of bacteria was increasing. He was thinking what would be the number of bacteria after 100 hours if this pattern continues. When he asked his teacher about the same the answer he got was the concept of an exponential function.
Let us learn more about exponential function along with its definition, equation, graphs, exponential growth, exponential decay, etc.
What is Exponential Function?
Exponential function, as its name suggests, involves exponents. But note that, an exponential function has a constant as its base and a variable as its exponent but not the other way round (if a function has a variable as the base and a constant as the exponent then it is a power function but not an exponential function). An exponential function can be in one of the following forms.
Exponential Function Definition
In mathematics, an exponential function is a function of form f (x) = ax, where “x” is a variable and “a” is a constant which is called the base of the function and it should be greater than 0.

Exponential Function Examples
Here are some examples of exponential function.
- f(x) = 2x
- f(x) = (1/2)x
- f(x) = 3e2x
- f(x) = 4 (3)-0.5x
Exponential Function Formula
A basic exponential function, from its definition, is of the form f(x) = bx, where 'b' is a constant and 'x' is a variable. One of the popular exponential functions is f(x) = ex, where 'e' is "Euler's number" and e = 2.718....If we extend the possibilities of different exponential functions, an exponential function may involve a constant as a multiple of the variable in its power. i.e., an exponential function can also be of the form f(x) = ekx. Further, it can also be of the form f(x) = p ekx, where 'p' is a constant. Thus, an exponential function can be in one of the following forms.
- f(x) = bx
- f(x) = abx
- f(x) = abcx
- f(x) = ex
- f(x) = ekx
- f(x) = p ekx
Here, apart from 'x' all other letters are constants, 'x' is a variable, and f(x) is an exponential function in terms of x. Also, note that the base in each exponential function must be a positive number. i.e., in the above functions, b > 0 and e > 0. Also, b should not be equal to 1 (if b = 1, then the function f(x) = bx becomes f(x) = 1 and in this case, the function is linear but NOT exponential).
The exponential function arises whenever a quantity's value increases in exponential growth and decreases in exponential decay. We can see more differences between exponential growth and decay along with their formulas in the following table.
| Exponential Growth | Exponential Decay |
|---|---|
| In exponential growth, a quantity slowly increases in the beginning and then it increases rapidly. | In exponential decay, a quantity decreases very rapidly in the beginning, and then it decreases slowly. |
| The exponential growth formulas are used to model population growth, to model compound interest, to find doubling time, etc | The exponential decay is helpful to model population decay, to find half-life, etc. |
| The graph of the function in exponential growth is increasing. | The graph of the function in exponential growth is decreasing. |
|
In exponential growth, the function can be of the form:
Here, b = 1 + r ≈ ek. |
In exponential decay, the function can be of the form:
Here, b = 1 - r ≈ e- k. |
In the above formulas,
- a (or) P0 = Initial value
- r = Rate of growth
- k = constant of proportionality
- x (or) t = time (time can be in years, days, (or) months. Whatever we are using should be consistent throughout the problem).
Exponential Function Graph
We can understand the process of graphing exponential function by taking some examples. Let us graph two functions f(x) = 2x and g(x) = (1/2)x. To graph each of these functions, we will construct a table of values with some random values of x, plot the points on the graph, connect them by a curve, and extend the curve on both ends. The process of graphing exponential function can be learned in detail by clicking here.
Here is the table of values that are used to graph the exponential function f(x) = 2x.

Here is the table of values that are used to graph the exponential function g(x) = (1/2)x.
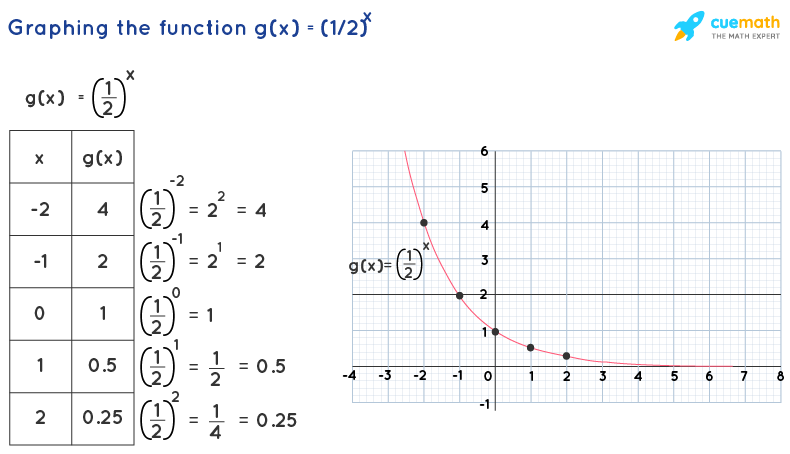
Note: From the above two graphs, we can see that f(x) = 2x is increasing whereas g(x) = (1/2)x is decreasing. Thus, the graph of exponential function f(x) = bx.
- increases when b > 1
- decreases when 0 < b < 1
Exponential Function Asymptotes
The exponential function has no vertical asymptote as the function is continuously increasing/decreasing. But it has a horizontal asymptote. The equation of horizontal asymptote of an exponential funtion f(x) = abx + c is always y = c. i.e., it is nothing but "y = constant being added to the exponent part of the function". In the above two graphs (of f(x) = 2x and g(x) = (1/2)x), we can notice that the horizontal asymptote is y = 0 as nothing is being added to the exponent part in both the functions. Thus,
- An exponential function never has a vertical asymptote.
- The horizontal asymptote of an exponential function f(x) = abx + c is y = c.
Domain and Range of Exponential Function
We know that the domain of a function y = f(x) is the set of all x-values (inputs) where it can be computed and the range is the set of all y-values (outputs) of the function. From the graphs of f(x) = 2x and g(x) = (1/2)x in the previous section, we can see that an exponential function can be computed at all values of x. Thus, the domain of an exponential function is the set of all real numbers (or) (-∞, ∞). The range of an exponential function can be determined by the horizontal asymptote of the graph, say, y = d, and by seeing whether the graph is above y = d or below y = d. Thus, for an exponential function f(x) = abx,
- Domain is the set of all real numbers (or) (-∞, ∞).
- Range is f(x) > d if a > 0 and f(x) < d if a < 0.
To understand this, you can see the example below.

Exponential Series
The real exponential function can be commonly defined by the following power series,
ex = Σn = 0∞ xn/n! = 1 + (x/1) + (x2/2) + (x3/6) + ...
Expansion of some other exponential functions are given as shown below,
e = Σn = 0∞ 1n/n! = 1 + (1/1) + (1/2) + (1/6) + ...
e-1 = Σn = 0∞ (-1)n/n! = 1 - (1/1) + (1/2) - (1/6) + ...
Exponential Function Rules
The rules of exponential function are as same as that of rules of exponents. Here are some rules of exponents.
- Law of Zero Exponent: a0 = 1
- Law of Product: am × an = am+n
- Law of Quotient: am/an = am-n
- Law of Power of a Power: (am)n = amn
- Law of Power of a Product: (ab)m = ambm
- Law of Power of a Quotient: (a/b)m = am/bm
- Law of Negative Exponent: a-m = 1/am
Apart from these, we sometimes need to use the conversion formula of logarithmic form to exponential form which is:
- bx = a ⇔ logb a = x
Equality Property of Exponential Function
According to the equality property of exponential function, if two exponential functions of the same bases are the same, then their exponents are also the same. i.e.,
bx1 = bx2 ⇔ x1 = x2
Exponential Function Derivative
Here are the formulas from differentiation that are used to find the derivative of exponential function.
- d/dx (ex) = ex
- d/dx (ax) = ax · ln a.
Integration of Exponential Function
Here are the formulas from integration that are used to find the integral of exponential function.
- ∫ ex dx = ex + C
- ∫ ax dx = ax / (ln a) + C
Important Notes on Exponential Function:
- The domain of any exponential function is the set of all real numbers.
- An exponential function has no vertical asymptote.
- Every exponential function has one horizontal asymptote.
- The graph of any exponential function is either increasing or decreasing.
☛ Related Topics:
Examples on Exponential Function
-
Example 1: In 2010, there were 100,000 citizens in a town. If the population increases by 8% every year, then how many citizens will there be in 10 years? Round your answer to the nearest integer.
Solution:
The initial population is, a = 100,000.
The rate of growth is, r = 8% = 0.08.
The time is, x = 10 years.
Using the exponential growth formula,
f(x) = a (1 + r)x
f(x) = 100000(1 + 0.08)10
f(x) ≈ 215,892 (rounded to the nearest integer)
Answer: Therefore, the number of citizens in 10 years will be 215,892.
-
Example 2: The half-life of carbon-14 is 5,730 years. If there were 1000 grams of carbon initially, then what is the amount of carbon left after 2000 years? Round your answer to the nearest integer.
Solution:
Using the given data, we can say that carbon-14 is decaying and hence we use the formula of exponential decay.
P = P0 e- k t ... (1),
Here, P0 = initial amount of carbon = 1000 grams.
It is given that the half-life of carbon-14 is 5,730 years. It means
P = P0 / 2 = 1000 / 2 = 500 grams.
Substitute all these values in (1),
500 = 1000 e- k (5730)
Dividing both sides by 1000,
0.5 = e- k (5730)
Taking "ln" on both sides,
ln 0.5 = -5730k
Dividing both sides by -5730,
k = ln 0.5 / (-5730) ≈ 0.00012097
We have to find the amount of carbon that is left after 2000 years. Substitute t = 2000 in (1),
P = 1000 e- (0.00012097) (2000) ≈ 785 grams.
Answer: The amount of carbon left after 1000 years = 785 grams.
-
Example 3: Simplify the following exponential expression: 3x - 3x+2
Solution:
Given exponential equation: 3x - 3x+2
By using the property: ax ay = ax+y
Hence, 3x+2 can be written as 3x.32
Thus the given equation is written as:
3x - 3x+2 = 3x - 3x·9
Now, factor out the term 3x
3x - 3x+2 = 3x - 3x·9 = 3x(1 - 9)
3x - 3x+2 = 3x(-8)
3x - 3x+2 = -8(3x)
Answer: Therefore, the simplification of the given expoential equation 3x-3x+1 is -8(3x).

FAQs on Exponential Function
What is the Definition of Exponential Function?
An exponential function is a type of function in math that involves exponents. A basic exponential function is of the form f(x) = bx, where b > 0 and b ≠ 1.
What are the Formulas of Exponential Function?
The formulas of an exponential function have exponents in them. An exponential equation can be in one of the following forms.
- f(x) = abcx
- f(x) = p ekx
What are the Rules of Exponential Function?
Since the exponential function involves exponents, the rules of exponential function are as same as the rules of exponents. They are:
- am × an = am+n
- am/an = am-n
- a0 = 1
- a-m = 1/am
- (am)n = amn
- (ab)m = ambm
- (a/b)m = am/bm
How to Graph Exponential Function?
To graph an exponential function y = f(x), create a table of values by taking some random numbers for x (usually we take -2, -1, 0, 1, and 2), and substitute each of them in the function to find the corresponding y values. Then plot the points from the table and join them by a curve. Finally, extend the curve on both ends. Keep a note of horizontal asymptote while drawing the graph.
What is the Domain of Exponential Function?
An exponential function f(x) = abx is defined for all values of x and hence its domain is the set of all real numbers, which in interval notation can be written as (-∞, ∞).
What are the Properties of Exponential Function?
The properties of exponential function can be given as,
- am × an = am+n
- am/an = am-n
- a0 = 1
- a-m = 1/am
- (am)n = amn
- (ab)m = ambm
- (a/b)m = am/bm
For any exponential function of the form f(x) = abx, where b > 1, the exponential graph increases while for any exponential function of the form f(x) = abx, where 0 < b < 1, the graph decreases.
What is the Range of Exponential Function?
The range of an exponential function depends upon its horizontal asymptote and also whether the curve lies above or below the horizontal asymptote. i.e., for an exponential function f(x) = abx, the range is
- f(x) > d if a > 0 and
- f(x) < d if a < 0,
where y = d is the horizontal asymptote of the graph of the function.
What is the Equality Property of Exponential Function?
The equality property of exponential function says if two values (outputs) of an exponential function are equal, then the corresponding inputs are also equal. i.e., bx1 = bx2 ⇔ x1 = x2.
What is the Derivative of Exponential Function?
An exponential function may be of the form ex or ax. The formulas to find the derivatives of these functions are as follows:
- The derivative of ex is, d/dx (ex) = ex
- d/dx (ax) = ax · ln a.
What is the Integral of Exponential Function?
An exponential function may be of the form ex or ax. The formulas to find the integrals of these functions are as follows:
- The integral of ex is, ∫ ex dx = ex + C
- ∫ ax dx = ax / (ln a) + C
visual curriculum