Skew Symmetric Matrix

In mathematics, a skew symmetric matrix is defined as the square matrix that is equal to the negative of its transpose matrix. For any square matrix, A, the transpose matrix is given as A^T. A skew-symmetric or antisymmetric matrix A can therefore be represented as, A = -A^T. A skew-symmetric matrix finds application in various fields, such as, in machine learning and in statistical analysis.

Let us learn about skew symmetric matrix, their definitions, and properties using solved examples in the following sections.

1.	What is Skew Symmetric Matrix?
2.	Properties of Skew Symmetric Matrix
3.	Theorems Related to Skew Symmetric Matrix
4.	Determinant of Skew Symmetric Matrix
5.	Eigen Value of Skew Symmetric Matrix
6.	Trace of Skew Symmetric Matrices
7.	FAQs on Symmetric and Skew Matrices

A skew symmetric matrix is a square matrix that is equal to the negative of its transpose matrix. It is important to know the method to find the transpose of a matrix, in order to understand a skew-symmetric matrix better. Here, we have considered a matrix A. The basic formula representing a Skew Symmetric Matrix is as follows.

B = -B^T

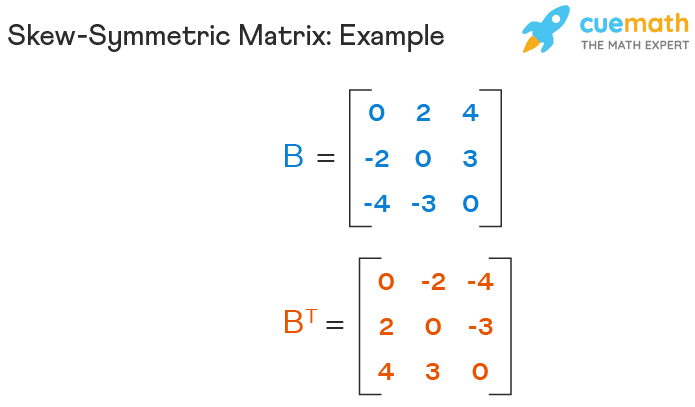
Skew Symmetric Matrix Definition

A square matrix B which of size n × n is considered to be a skew symmetric matrix if and only if B^T = -B. That is, the transposed form of a skew symmetric or antisymmetric matrix that is equal to the negative of that matrix. This can be represented as:

If B = \(\left[\mathrm{b}_{\mathrm{ij}}\right]_{\mathrm{n} \times \mathrm{n}} \) is the skew symmetric matrix, then \(b_{ij}\) = -\(b_{ji}\) for all i and j or 1 ≤ i ≤ n, and 1 ≤ j ≤ n. Here, n is any natural number. If we put i = j, then \(b_{ii}\) = 0 for all i. This means that all elements that are present diagonally in a skew-symmetric matrix are zero.

Skew Symmetric Matrix Example:

Let’s take an example of a matrix B,

\(
\begin{array}{l}
B = \left[\begin{array}{cc}
0 & 3 \\ \\
-3 & 0
\end{array}\right] \\
B^{T} = \left[\begin{array}{cc}
0 & -3 \\ \\
3 & 0
\end{array}\right] \\
-B = -\left[\begin{array}{cc}
0 & 3 \\ \\
-3 & 0
\end{array}\right] \\
-B = \left[\begin{array}{cc}
0 & -3 \\ \\
3 & 0
\end{array}\right]
\end{array}\)

Here, we can see that, B^T = -B, \(b_{12}\) = -\(b_{21}\), and \(b_{11}\) = \(b_{22}\) = 0. Thus, B is a skew symmetric matrix.

The two important conditions for a matrix to be skew symmetric are that it should be a square matrix i.e., the number of rows and columns should be equal and secondly, the given matrix should be equal to the negative of its transpose. Here are some of the important properties of a skew-symmetric matrix,

• When two skew-symmetric matrices are added, then the resultant matrix will always be a skew-symmetric matrix. Consider two skew symmetric matrices A and B such that A^T = -A, and B^T= -B, then we have (A + B)^T = -(A + B)
• The trace of a skew symmetric matrix equals zero i.e., the sum of all the elements in the main diagonal is also equal to zero.
• The real eigenvalue of a real skew symmetric matrix A, λ equal zero. That means the nonzero eigenvalues of a skew-symmetric matrix are non-real.
• When a scalar or a real number is multiplied with a skew-symmetric matrix, the resultant matrix will also be a skew-symmetric matrix. Consider a scalar value k, B is a skew-symmetric matrix, then the resultant matrix is also a skew symmetric matrix. ( kB)^T = -kB.
• For any real skew symmetric matrix A, I + A matrix will be invertible, where I is an identity matrix.
• For any real skew symmetric matrix, A, A² is a symmetric negative semi-definite matrix.

There are two important theorems related to skew symmetric matrices. In this section, let's learn about these theorems along with their proofs.

Theorem 1: For any square matrix A with real number elements, A + A^T is a symmetric matrix, and A - A^T is a skew-symmetric matrix.

Proof:

Let P = A + A^T.

Transpose of P can be given as, P^T = ( A + A^T )^T = A^T + ( A^T )^T = A^T + A = A + A^T = P

⇒ A + A^T is a symmetric matrix.

Next, we let Q = A - A^T

Q^T = ( A + ( -A^T ))^T = A^T + ( -A^T )^T = A^T - ( A^T )^T = A^T - A = -( A - A^T ) = -Q

⇒ A − A^T is a skew-symmetric matrix.

Theorem 2: Any square matrix A can be expressed as the sum of a symmetric matrix, S and a skew symmetric matrix, V, such that,

A = (1/2) × (A + A^T) + (1/2 ) × (A - A^T). Here, A^T is the transpose of the square matrix A.

• If A + A^T is a symmetric matrix, then (1/2) × (A + A^T) is also a symmetric matrix.
• If A - A^T is a skew symmetric matrix, then (1/2 ) × (A - A^T) is also a skew symmetric matrix.

Thus, any square matrix can be expressed as the sum of a skew symmetric matrix and a symmetric matrix

The determinant of a skew-symmetric matrix having an order equal to an odd number is equal to zero. So, if we see any skew-symmetric matrix whose order is odd, then we can directly write its determinant equal to 0.

Let's verify this property using a 3×3 matrix as follows:

\(B = \left[\begin{array}{ccc}
0 & a & b \\
-a & 0 & m \\
-b & -m & 0
\end{array}\right] \)

Let's find the determinant of B as, |B| = 0 (cofactor of \(b_{11}\)) + a (cofactor of \(b_{12}\)) + b (cofactor of \(b_{13}\))

= a (cofactor of \(b_{12}\)) + b (cofactor of \(b_{13}\))

= a ((-1)¹⁺² (0-(-bm))) + b ((-1)¹⁺³ (am))

= a(-1)³(bm) + b(1)⁴(am)

= a(-1)(bm) + b(1)(am)

= -abm + abm

= 0

Therefore, we can conclude that the determinant of a skew symmetric matrix whose order is odd, will always be zero.

The eigenvalues of a skew symmetric matrix are either zero or imaginary values. The real eigenvalue of a real skew symmetric matrix A, λ equal zero, that means the nonzero eigenvalues of a skew-symmetric matrix are non-real.

Proof: Let A be a square matrix and λ be an eigenvalue of A and x be an eigenvector corresponding to the eigenvalue λ.

⇒ Ax = λx.

Multiplying both sides by x̅^T(x̅ is conjugate of eigen vector x), we get,

x̅^TAx = λ x̅^Tx = λ||x||².

Note that the term x̅^TAx is the dot (inner) product of x̅ and Ax. Since the dot product is commutative, we have, x̅^TAx = (Ax)^Tx̅ = x^TA^Tx̅.

Since A is skew-symmetric, we have A^T = -A. Substituting this into the above equation, we get,

x^TA^Tx̅ = -x^TAx̅

Taking conjugate of Ax = λx and use the fact that A is real, we have

Ax̅ = \(\overlineλ\)x̅

Thus, we have

-x^TAx̅ = -x^T\(\overlineλ\)x̅ = -\(\overlineλ\)||x||².

-\(\overlineλ\)||x||² = λ||x||²

Since x is an eigenvector, it is nonzero by definition. Thus ||x|| ≠ 0. Hence we have, -\(\overlineλ\) = λ,
⇒ λ is either 0 or a purely imaginary number.

The trace of a matrix is defined as the sum of all its diagonal elements. As discussed under the properties of a skew-symmetric matrix, the diagonal elements of a skew symmetric matrix are zero. Therefore, the trace of a skew symmetric matrix always equals zero.

Important Notes on Skew Symmetric Matrix:

Here is a list of a few points that should be remembered while studying skew symmetric matrix.

• A matrix for which the transposed form is equal to the negative of the original matrix is called a skew-symmetric matrix.
• Any matrix can be expresses as a sum of a symmetric and a skew-symmetric matrix. For a square matrix A, A = (1/2)(A + A^T) + (1/2)(A - A^T).
• If the order of a skew-symmetric matrix is odd, then its determinant is equal to zero.

☛ Related Topics:

Check out the following pages related to skew symmetric matrix.

• Matrix Calculator
• Matrix formula
• Diagonal Matrix Calculator
• Transpose Matrix Calculator

 

What are Skew Symmetric Matrices?

A skew-symmetric matrix is a matrix whose transposed form is equal to the negative of that matrix. This is an example of a skew-symmetric matrix:

\(B=\left[\begin{array}{ll}
0 & 2\\
-2 & 0
\end{array}\right]\)

What Are the Properties Skew Symmetric Matrix?

These are the important properties of skew symmetric matrix:

• When two skew-symmetric matrices are added, then the resultant matrix will always be a skew-symmetric matrix.
• Since the elements that are present on the diagonal of a skew-symmetric matrix are zero, its trace also equals zero i.e., the sum of all the elements in the main diagonal is also equal to zero
• When one identity matrix is added to a skew symmetric matrix, then the resultant matrix is an invertible matrix.
• When a scalar or a real number is multiplied with a skew symmetric matrix, the resultant matrix will also be a skew-symmetric matrix.

How to Check if a Matric is Skew Symmetric Matrix?

To check if a matrix is skew symmetric matrix, we find the transpose of the given matrix. If the obtained transposed matrix is equal to the negative of the original matrix, then the given matrix is skew symmetric matrix.

How Do You Know if a Matrix is Both Symmetric and Skew Symmetric Matrix?

A null matrix or a zero matrix is the only matrix that is both symmetric and skew symmetric. Any matrix whose rows and columns are all zeroes can be considered as both symmetric and skew symmetric matrix.

Give an Example of a Matrix That is Both Symmetric and Skew Symmetric Matrix.

Consider the given matrix:

\(A=\left[\begin{array}{ll}
0 & 0\\ \\
0 & 0
\end{array}\right]\)

The matrix given above is a null matrix and this is the only matrix that is both symmetric and skew symmetric.

What is the Sum of a Symmetric and Skew Symmetric Matrix?

We know from the properties of the symmetric and skew symmetric matrices that the sum of any symmetric and a skew symmetric matrix is always a square matrix. Given A is a square matrix then, A = (1/2) × (A + A^T) + (1/2 ) × (A - A^T). Here, A^T is the transpose of the square matrix A, A + A^T is a symmetric matrix, and A - A^T is a skew-symmetric matrix.

What Is the Sum of Two Skew Symmetric Matrices?

As per the properties of the skew symmetric matrices, the sum of any two skew symmetric matrices will always be a skew symmetric matrix. Consider two skew symmetric matrices A and B, then A + B = C, C will also be a skew symmetric matrix.

How Do You Find a Skew Symmetric Matrix?

These are the steps to find a skew symmetric matrix:

• Step 1: Firstly, check if it's a square matrix, as only square matrices can be considered as skew symmetric matrices.
• Step 2: Find the transpose of the given matrix.
• Step 3: Then find the negative of the given matrix.
• Step 4: If the transpose of the matrix is equal to the negative of the given matrix, then it is a skew symmetric matrix.