Vector Addition
Vector addition finds its application in physical quantities where vectors are used to represent velocity, displacement, and acceleration.
- Adding the vectors geometrically is putting their tails together and thereby constructing a parallelogram. The sum of the vectors is the diagonal of the parallelogram that starts from the intersection of the tails.
- Adding vectors algebraically is adding their corresponding components.
In this article, let's learn about the addition of vectors, their properties, and various laws with solved examples.
What is the Vector Addition?
Vectors are represented as a combination of direction and magnitude and are written with an alphabet and an arrow over them (or) with an alphabet written in bold. Two vectors, a and b, can be added together using vector addition, and the resultant vector can be written as: a + b. Before learning about the properties of vector addition, we need to know about the conditions that are to be followed while adding vectors. The conditions are as follows:
- Vectors can be added only if they are of the same nature. For instance, acceleration should be added with only acceleration and not mass
- We cannot add vectors and scalars together
Consider two vectors C and D, where, C = Cxi + Cyj + Czk and D = Dxi + Dyj + Dzk. Then, the resultant vector (or vector sum formula) is R = C + D = (Cx + Dx)i + (Cy + Dy)j + (Cz + Cz) k
Properties of Vector Addition
Vector addition is different from algebraic addition. Here are some of the important properties to be considered while doing vector addition:
| Property of Vector Addition | Explanation |
|---|---|
| Existence of identity |
For any vector v, v + 0 = v Here, 0 vector is the additive identity. |
| Existence of inverse |
For any vector v, v + - v = 0 and thus an additive inverse exists for every vector. |
| Commutativity |
Addition is commutative; for any two arbitrary vectors c, and d, c + d = d + c |
| Associativity |
Addition is associative; for any three arbitrary vectors i, j, and k , i + j + k = i + j + k i.e, the order of addition does not matter. |
Addition of Vectors Graphically
Vectors adding can be done using graphical and mathematical methods. These methods are as follows:
- Vector Addition Using the Components
- Triangle Law of Addition of Vectors
- Parallelogram Law of Addition of Vectors
Vector Addition Using the Components
Vectors that are represented in cartesian coordinates can be decomposed into vertical and horizontal components. For instance, a vector A at an angle Φ, as shown in the below-given image, can be decomposed into its vertical and horizontal components as:
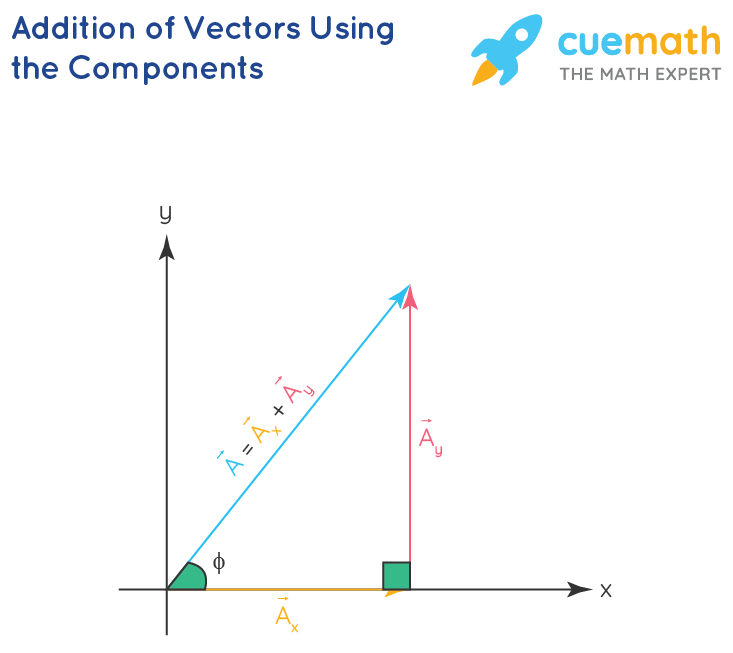
In the above image,
- Ax, represents the component of vector A along the horizontal axis (x-axis), and
- Ay, represents the component of vector A along the vertical axis (y-axis).
We can note that the three vectors form a right triangle and that the vector A can be expressed as:
A = Ax + Ay
Mathematically, using the magnitude and the angle of the given vector, we can determine the components of a vector.
Ax = A cos Φ
Ay = A sin Φ
For two vectors, if its horizontal and vertical components are given, then the resultant vector can be calculated. For instance, if the values of Ax and Ay are provided, then we will be able to calculate the angle and the magnitude of the vector A as follows:
|A| = √ ((Ax)2+(Ay)2)
And the angle can be found as:
Φ = tan-1 (Ay/ Ax)
Hence, we can conclude that:
- If the components of a vector are provided, then we can determine the resultant vector
- Likewise, we can determine the components of a vector using the above equations, if the vector is provided
Similarly, we can perform the addition on vectors using their components, if these vectors are expressed in ordered pairs i.e column vectors. For example, consider the two vectors P and Q.
P = (p1, p2)
Q = (q1, q2)
The resultant vector M can be obtained by performing vector addition on the two vectors P and Q, by adding the respective x and y components of these two vectors.
M = P + Q
M = (p1+q1, p2+ q2).
This can be expressed explicitly as:
Mx = p1 + q1
My = p2 + q2.
The magnitude formula to find the magnitude of the resultant vector M is: |M| = √ ((Mx)2+(My)2)
And the angle can be computed as Φ = tan-1 (My/ Mx)
Laws of Vector Addition
There are two laws of vector addition (As mentioned in the previous section).
Using these two laws, we are going to prove that the sum of two vectors is obtained by attaching them head to tail and the vector sum is given by the vector that joins the free tail and free head. Let us study each of these laws in detail in the upcoming sections.
Triangle Law of Addition of Vectors
The famous triangle law can be used for the addition of vectors and this method is also called the head-to-tail method. As per this law, two vectors can be added together by placing them together in such a way that the first vector’s head joins the tail of the second vector. Thus, by joining the first vector’s tail to the head of the second vector, we can obtain the resultant vector sum. The addition of vectors using the triangle law can be with the following steps:
- First, the two vectors M and N are placed together in such a manner that the head of vector M connects the tail of vector N.
- And then, in order to find the sum, a resultant vector S is drawn in such a way that it connects the tail of M to the head of N.
- Thus, mathematically, the sum, or the resultant, vector S, in the below-given image can be expressed as S = M + N.

Thus, when the two vectors M and N are added using the triangle law, we can see that a triangle is formed by the two original vectors M and N, and the sum vector S.
Parallelogram Law of Addition of Vectors
Another law that can be used for the addition of vectors is the parallelogram law of the addition of vectors. Let’s take two vectors p and q, as shown below. They form the two adjacent sides of a parallelogram in their magnitude and direction. The sum p + q is represented in magnitude and direction by the diagonal of the parallelogram through their common point. This is the parallelogram law of vector addition.

In the above-given figure, using the Triangle law, we can conclude the following:
OP + PR = OR
OP + OQ = OR, since PR = OQ
Hence, we can conclude that the triangle laws of vector addition and the parallelogram law of vector addition are equivalent to each other.
Vector Addition Formulas
We use one of the following formulas to add two vectors a = <a1, a2, a3> and b = <b1, b2, b3>.
- If the vectors are in the component form then the vector sum formula is a + b = <a1 + b1, a2 + b2, a3 + b3>.
- If the two vectors are arranged by attaching the head of one vector to the tail of the other, then their sum is the vector that joins the free head and free tail (by triangle law).
- If the two vectors represent the two adjacent sides of a parallelogram then the sum represents the diagonal vector that is drawn from the common point of both vectors (by parallelogram law).
Important Notes on Vector Addition:
Here is a list of a few points that should be remembered while studying the addition of vectors:
- Vectors are represented as a combination of direction and magnitude and they are drawn with an arrow representation.
- If the components of a vector are provided, then we can determine the resultant vector.
- The famous triangle law can be used for the addition of vectors and this method is also called the head-to-tail method.
☛Related Articles:
Check out the following pages related to the addition of vectors:
Examples of Addition of Vectors
-
Example 1: Find the addition of vectors PQ and QR, where PQ = (3, 4) and QR = (2, 6)
Solution:
We will perform the vector addition by adding their corresponding components
PQ + QR = (3, 4) + (2, 6)
= (3 + 2, 4 + 6)
= (5, 10).
Answer: (5, 10).
-
Example 2: Two vectors are given along with their components: A = (2,3) and B = (2,-2). Calculate the magnitude and the angle of the sum C using their components.
Solution:
Let us represent the components of the given vectors as:
- In the A, Ax = 2 and Ay = 3
- In the B, Bx = 2 and By = -2
Now, adding the two vectors,
A + B = (2, 3) + (2, -2) = (4, 1)
It can also be written as:
C = (4, 1)
Here in C, Cx = 4 and Cy = 1
The magnitude of the resultant vector C can be calculated as:
|C| = √ ((Cx)2+(Cy)2)
|C| = √ ((4)2 + (1)2)
= √ (16 + 1)
|C| = √ 17 = 4.123 units (Approximately)
And the angle can be calculated as follows:
Φ = tan-1 (Cy/ Cx)
Φ = tan-1 (1/4)
Φ ≈ 14.04 degrees
Answer: Thus, the magnitude of the resultant vector |C| = 4.123 units (Approximately) and the angle Φ = 14.04 degrees
-
Example 3: If a = <1, -1> and b = <2, 1> then find the unit vector in the direction of addition of vectors a and b.
Solution:
The vector sum is:
a + b = <1, -1> + <2, 1> = <1 + 2, -1 + 1> = <3, 0>
Its magnitude is, |a + b| = √(32 + 02) = √9 = 3.
The unit vector in the direction of vector addition is:
(a + b) / |a + b| = <3, 0> / 3 = <1, 0>
Answer: The required unit vector is, <1, 0>.

FAQs on Vector Addition
What is the Addition of Vectors?
The addition of vectors means putting two or more vectors together. In the addition of vectors, we are adding two or more vectors using the addition operation in order to obtain a new vector that is equal to the sum of the two or more vectors. The sum of vectors a and b is written as a + b.
Example: Given two vectors, a = (2, 5) and b = (4, -2), the sum of vectors is (6,3)
What is the Formula For the Addition of Vectors?
This is the addition of vectors formula: Given two vectors a = (a1, a2) and b = (b1, b2), then the vector sum is, M = (a1 + b1, a2 + b2) = (Mx, My). In this case,
- magnitude of the resultant vector sum M = |M| = √ ((Mx)2+(My)2) and
- the angle can be computed as θ = tan-1 (My/ Mx)
What is the Vector Addition Rule?
To add two vectors that are in component form, we just add their corresponding components. To add two vectors geometrically, we use triangle law or parallelogram law.
What is the Formula of Parallelogram Law of Addition of Vectors?
As per the parallelogram law of addition of vectors, for two given vectors u and v enclosing an angle θ, the magnitude of the sum, |u + v|, is given by √(u2+v2+2uvcos(θ)).
What is the Difference Between Vector addition and Subtraction?
Here are the differences between addition of vectors and the subtraction of vectors.
| Addition of Vectors | Subtraction of Vectors |
|---|---|
| We denote the sum of vectors a and b as a + b. | We denote the difference of vectors a and b as a - b. |
| Vector addition is commutative. | Vector subtraction is NOT commutative. |
| Vector addition is associative. | Vector subtraction is NOT associative. |
| We have to place the vectors such that their tails touch each other to add them. | We add the negative of b to a to find a - b. |
Is Addition of Vectors Commutative?
Yes, vectors adding is commutative; for any two arbitrary vectors c, and d, c + d = d + c.
What is the Difference Between the Triangle Law of Vector Addition and the Parallelogram Law of Vector Addition?
For any two given vectors, as per the triangle law of vector addition, the third side of the triangle will become the resultant sum vector. Whereas, as per the parallelogram law of vector addition, the diagonal becomes the resultant sum vector.
What is the Associative Property of Addition of Vectors?
Addition is associative; for any three arbitrary vectors a, b, and c, a + (b + c) = (a + b) + c. i.e, the order of addition does not matter.
What is the Triangle Law of Addition of Vectors?
The triangle law of the addition of vectors states that two vectors can be added together by placing them together in such a way that the first vector’s head joins the tail of the second vector. Thus, by joining the first vector’s tail to the head of the second vector, we can obtain the resultant sum vector.
visual curriculum