Congruent Lines
Congruent lines in geometry refer to the segments which are identical in their measure. They are 1- dimensional superimposable segments having equal lengths. Congruent lines can have different alignments and orientations. We will be studying the properties and theorems of congruent lines in this article.
| 1. | What are Congruent Lines Segments? |
| 2. | Congruent Segments Properties |
| 3. | FAQs on Congruent Lines |
What are Congruent Line Segments?
Congruent line segments are 1-dimensional geometrical figures having equal measures. The word "congruent" with respect to congruent lines in geometry is defined as the equality between the two line segments. Two lines are said to be congruent when they have the same length. Congruent segments are superimposable figures, which completely overlap when placed one over the other. On turning, flipping, or rotating the congruent segments, they still remain to be congruent. The symbol used to depict congruence between any two congruent line segments is ≅.
To brief it, congruent segments is just another name given to congruent line segments or congruent lines in geometry. All three terms are mathematically the same. Now, let us look into some examples of congruent line segments we find in mathematics.
Examples of congruent line segments:
- The radii of the same circle.
- Opposite sides of a parallelogram, rectangle, square, and rhombus.
- Sides of an equilateral triangle.
Let's look into the diagram below showing congruent line segments.
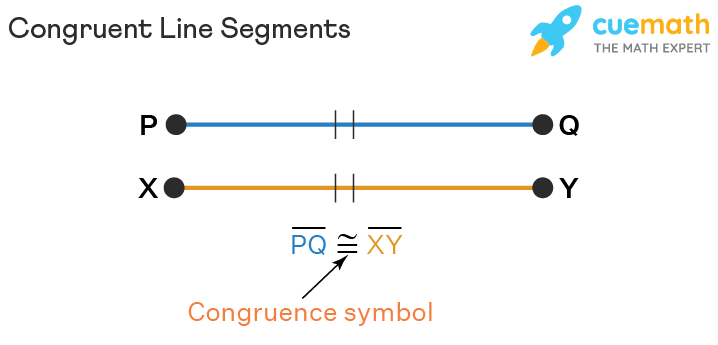
Here line segment PQ ≅ XY since the double vertical bars on each line segment, PQ and XY depict their equality.
Congruent Segments Properties
To understand more about the congruent line segments, we will be looking into their properties as listed below. The properties followed by congruent lines in geometry are:
(i) Reflexive
(ii) Symmetric
(iii) Transitive
Let us have a brief understanding of each of the properties individually.
Reflexive Property
Reflexive property is based on the principle of comparing an object to itself. It states that a line segment is always congruent to itself as the lengths remain the same. This can be understood by taking a real-time example. When the height of a pole is compared to itself, they are exactly equal and hence congruent. Therefore, the pole follows reflexive property.
Consider a line segment XY = 5cm. By Reflexive Property, XY ≅ XY.
Symmetric Property
Symmetric property is based on the principle that, if A = B then, B = A. It states that if a line segment is congruent to another line segment, then the second line segment is also congruent to the first line segment. To understand this better let's think about a practical scenario. If Ron's height is equal to Kelly's height then, Kelly's height is also equal to Ron's height.
Below is a pictorial representation that depicts the symmetric property of congruent lines.
From the above figure, the length of MN and EF is 8 cm.
Thus, by the symmetric property,
MN ≅ EF
EF ≅ MN
Transitive Property
Transitive property is based on the principle that, if A = B and B = C then, A = C. It states that, if a line segment is congruent to another line segment and the second line segment is congruent to the third line segment then, the first line segment is congruent to the third line segment.
Let's understand this better by looking into the diagram shown below.
From the above figure, we see that AB ≅ XY and XY ≅ PQ. Thus, using transitive property, we can conclude that AB ≅ PQ.
Related Articles on Congruent Lines
Check these articles related to the concept of congruent lines in geometry.
FAQs on Congruent Lines
What are Congruent Lines in Geometry?
Two line segments having lengths of equal measure are known as congruent lines. For example, if we have two line segments AB and PQ of 6 cm each, then we can say AB ≅ PQ and hence they are congruent.
What is the Definition of Congruent Line Segment?
A congruent line segment is defined as any line segment having equal measure. For example, the sides of an equilateral triangle are known as congruent line segments as all of them have the same measure.
When is a Line Segment Congruent to itself?
When a line segment is compared to itself, the line segment is congruent to itself since they exactly measure the same. This is the reflexive property followed by a congruent line segment. For example, consider a line segment, MN of length 7.5 cm. When this line segment is compared to itself they become congruent i.e., MN ≅ MN.
Why are Segments Congruent?
Segments are congruent due to their equality in length. The orientation or the inclination does not affect their congruency. Thus, two segments are congruent when they have equal lengths.
What are Congruent Lines Angles?
When two line segments exactly measure the same, they are known as congruent lines. For example, two line segments XY and AB have a length of 5 inches and are hence known as congruent lines. When two angles exactly measure the same, they are known as congruent angles. For example, the internal angles of a square are congruent as each angle measures 90º.
How to Prove two Line Segments are Congruent?
Given two line segments, the lengths can be measured using a ruler which helps us to compare their equality. If the lengths of two line segments are equal, they are known to be congruent. For example, sides of an equilateral triangle are congruent as all the three sides are of equal measure. The distance between two lines which are line segments and are congruent have a distance of zero units between them.
What is Congruent Segment Midpoint?
The congruent segment midpoint is defined as that point on a line segment that exactly divides the line segment into two parts of equal length and hence the two newly formed segments are congruent to each other. For example, for a line segment of length 10 cm, the midpoint will exactly be at 5 cm and the newly formed segments will be 5 cm each.