Conic Section
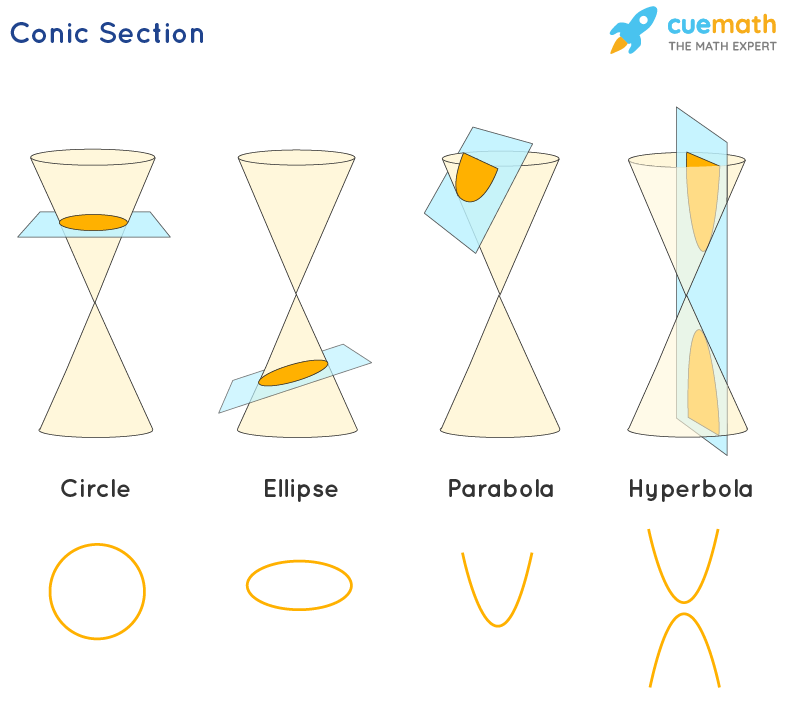
Conic sections or sections of a cone are the curves obtained by the intersection of a plane and cone. There are three major sections of a cone or conic sections: parabola, hyperbola, and ellipse(the circle is a special kind of ellipse). A cone with two identical nappes is used to produce the conic sections.
All the sections of a cone or conic sections have different shapes but they do share some common properties which we will read in the following sections. Let us check the conic section formulas, conic equations and its parameters, with examples, FAQs.
What Is Conic Section?
Conic sections are the curves obtained when a plane cuts the cone. A cone generally has two identical conical shapes known as nappes. We can get various shapes depending upon the angle of the cut between the plane and the cone and its nappe. By cutting a cone by a plane at different angles, we get the following shapes:
- Circle
- Parabola
- Ellipse
- Hyperbola
Ellipse is a conic section that is formed when a plane intersects with the cone at an angle. The circle is a special type of ellipse where the cutting plane is parallel to the base of the cone. A hyperbola is formed when the interesting plane is parallel to the axis of the cone, and intersect with both the nappes of the double cone. When the intersecting plane cuts at an angle to the surface of the cone, we get a conic section named parabola.
Conic Section Parameters
The focus, directrix, and eccentricity are the three important features or parameters which defined the conic. The various conic figures are the circle, ellipse, parabola, and hyperbola. And the shape and orientation of these shapes are completely based on these three important features. Let us learn in detail about each of them.
Focus
The focus or foci(plural) of a conic section is/are the point(s) about which the conic section is created. They are specially defined for each type of conic section. A parabola has one focus, while ellipses and hyperbolas have two foci. For an ellipse, the sum of the distance of the point on the ellipse from the two foci is constant. Circle, which is a special case of an ellipse, has both the foci at the same place and the distance of all points from the focus is constant. For parabola, it is a limiting case of an ellipse and has one focus at a distance from the vertex, and another focus at infinity. The hyperbola has two foci and the absolute difference of the distance of the point on the hyperbola from the two foci is constant.
Directrix
Directrix is a line used to define the conic sections. The directrix is a line drawn perpendicular to the axis of the referred conic. Every point on the conic is defined by the ratio of its distance from the directrix and the foci. The directrix is parallel to the conjugate axis and the latus rectum of the conic. A circle has no directrix. The parabola has 1 directrix, the ellipse and the hyperbola have 2 directrices each.
Eccentricity
The eccentricity of a conic section is the constant ratio of the distance of the point on the conic section from the focus and directrix. Eccentricity is used to uniquely define the shape of a conic section. It is a non-negative real number. Eccentricity is denoted by "e". If two conic sections have the same eccentricity, they will be similar. As eccentricity increases, the conic section deviates more and more from the shape of the circle. The value of e for different conic sections is as follows.
- For circle, e = 0.
- For ellipse, 0 ≤ e < 1
- For parabola, e = 1
- For hyperbola, e > 1
Terms Related To Conic Section
Other than these three parameters, conic sections have a few more parameters like principal axis, latus rectum, major and minor axis, focal parameter, etc. Let us briefly learn about each of these parameters related to the conic section. The following are the details of the parameters of the conic section.
- Principal Axis: The axis passing through the center and foci of a conic is its principal axis and is also referred to as the major axis of the conic.
- Conjugate Axis: The axis drawn perpendicular to the principal axis and passing through the center of the conic is the conjugate axis. The conjugate axis is also its minor axis.
- Center: The point of intersection of the principal axis and the conjugate axis of the conic is called the center of the conic.
- Vertex: The point on the axis where the conic cuts the axis is referred to as the vertex of the conic.
- Focal Chord: The focal chord of a conic is the chord passing through the focus of the conic section. The focal chord cuts the conic section at two distinct points.
- Focal Distance: The distance of a point \((x_1, y_1)\) on the conic, from any of the foci, is the focal distance. For an ellipse, hyperbola we have two foci, and hence we have two focal distances.
- Latus Rectum: It is a focal chord that is perpendicular to the axis of the conic. The length of the latus rectum for a parabola is LL' = 4a. And the length of the latus rectum for an ellipse, and hyperbola is 2b2/a.
-
Tangent: The tangent is a line touching the conic externally at one point on the conic. The point where the tangent touches the conic is called the point of contact. Also from an external point, about two tangents can be drawn to the conic.
-
Normal: The line drawn perpendicular to the tangent and passing through the point of contact and the focus of the conic is called the normal. We can have one normal for each of the tangents to the conic.
-
Chord of Contact: The chord drawn to join the point of contact of the tangents, drawn from an external point to the conic is called the chord of contact.
-
Pole and Polar: For a point which is referred as a pole and lying outside the conic section, the locus of the points of intersection of the tangents, draw at the ends of the chords, drawn from this point is called the polar.
- Auxilary Circle: A circle drawn on the major axis of the ellipse as its diameter is called the auxiliary circle. The conic equation of an ellipse is x2/a2 + y2/b2 = 1, and the equation of the auxiliary circle is x2 + y2 = a2.
- Director Circle: The locus of the point of intersection of the perpendicular tangents drawn to the ellipse is called the director circle. For an ellipse (x2/a2 + y2/b2 = 1), the equation of the director circle is x2 + y2 = a2 + b2
-
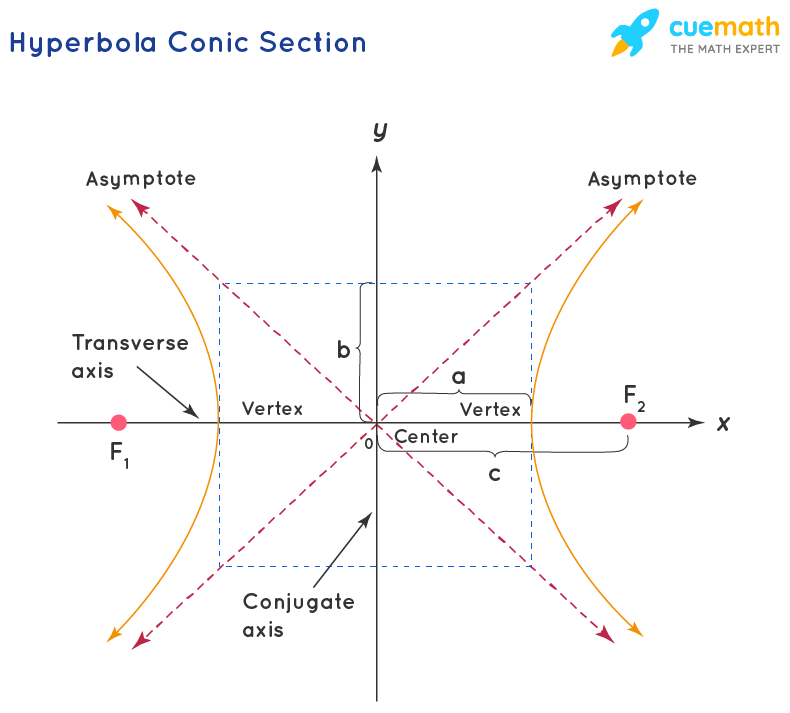
Asymptotes: The pair of straight lines drawn parallel to the hyperbola and assumed to touch the hyperbola at infinity. The equations of the asymptotes of the hyperbola are y = bx/a, and y = -bx/a respectively. And for a hyperbola having the conic equation of x2/a2 - y2/b2 = 1, the equation of the pair of asymptotes of the hyperbola are \(\dfrac{x}{a} ± \dfrac{y}{b} = 0\).
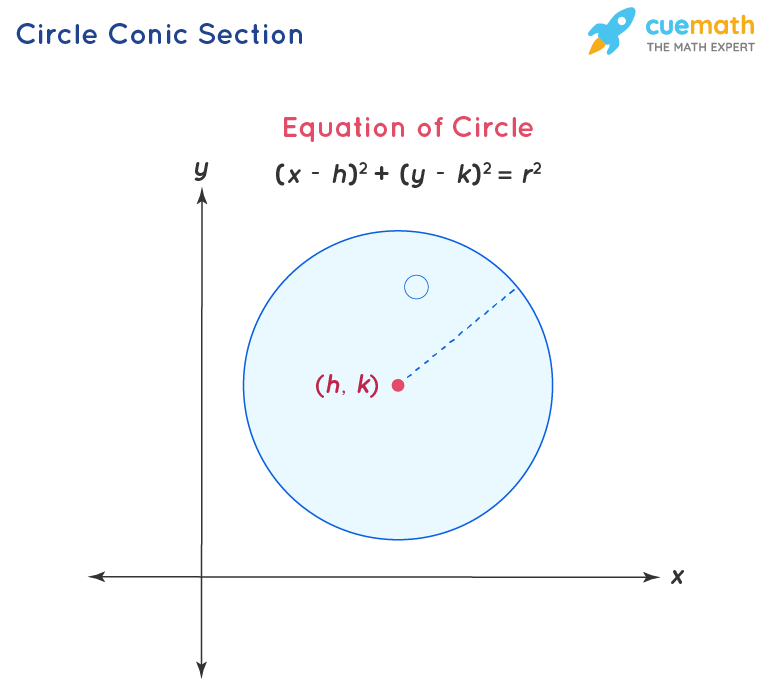
Circle - Conic Section
The circle is a special type of ellipse where the cutting plane is parallel to the base of the cone. The circle has a focus known as the center of the circle. The locus of the points on the circle have a fixed distance from the focus or center of the circle and is called the radius of the circle. The value of eccentricity(e) for a circle is e = 0. Circle has no directrix. The general form of the equation of a circle with center at (h, k), and radius r:
(x−h)2 + (y−k)2 = r2
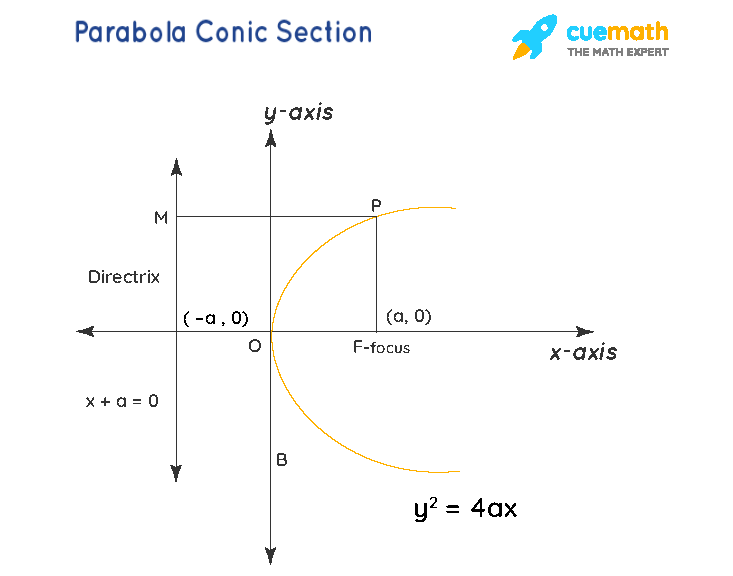
Parabola - Conic Section
When the intersecting plane is at an angle to the surface of the cone we get a conic section named parabola. It is a U-shaped conic section. The value of eccentricity(e) for parabola is e = 1. It is asymmetrical open plane curve formed by the intersection of a cone with a plane parallel to its side. The graph of a quadratic function is a parabola, a line-symmetric curve whose shape is like the graph of y = x2. The graph of a parabola either opens upward like y = x2 or opens downward like the graph of y = - x2. The path of a projectile under the influence of gravity ideally follows a curve of this shape.
Ellipse - Conic Section
Ellipse is a conic section that is formed when a plane intersects with the cone at an angle. Ellipse has 2 foci, a major axis, and a minor axis. Value of eccentricity(e) for ellipse is e < 1. Ellipse has 2 directrices. The general form of the equation of an ellipse with center at (h, k) and length of the major and minor axes as '2a' and '2b' respectively. The major axis of the ellipse is parallel to the x-axis. The conic section formula for an ellipse is as follows.
(x−h)2/a2 + (y−k)2/b2 = 1
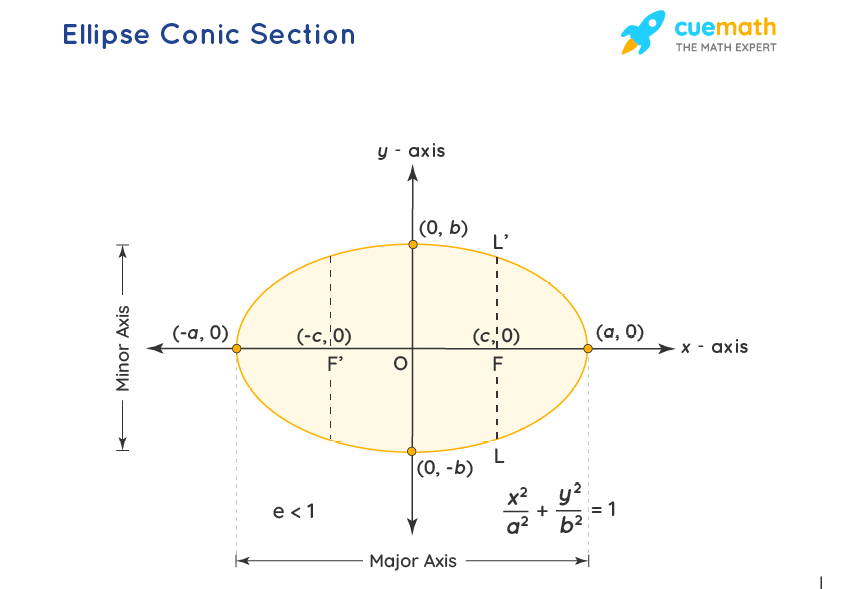
Note: If the major axis is parallel to the y-axis, switch the places of a and b in the above-given formula.
Hyperbola - Conic Section
A hyperbola is formed when the interesting plane is parallel to the axis of the cone, and intersect with both the nappes of the double cone. The value for eccentricity(e) for hyperbola is e > 1. The two unconnected sections of the hyperbola are called branches. They are mirror images of each other, and their diagonally opposite arms approach the limit to a line.
A hyperbola is an example of a conic section that can be drawn on a plane that intersects a double cone created from two nappes.The general form of the equation of the hyperbola with (h, k) as the center is as follows.
(x−h)2/a2 - (y−k)2/b2 = 1
Conic Section Formulas - Standard Forms
Conic section formulas represent the standard forms of a circle, parabola, ellipse, hyperbola. For ellipses and hyperbolas, the standard form has the x-axis as the principal axis and the origin (0,0) as the center. The vertices are (±a, 0) and the foci (±c, 0)., and is defined by the equations c2= a2 − b2 for an ellipse and c2 = a2 + b2 for a hyperbola. For a circle, c = 0 so a2 = b2. For the parabola, the standard form has the focus on the x-axis at the point (a, 0) and the directrix is the line with equation x = −a.
- Circle: x2+y2= a2
- Parabola: y2= 4ax when a>0
- Ellipse: x2/a2 + y2/b2 = 1
- Hyperbola: x2/a2 – y2/b2 = 1
Related Topics
Check out the articles below to know more about topics related to the intersection of two lines.
- Lines
- Parallel lines
- Equation of a Straight Line
- Slope-Intercept Form of a Line
- Point of Intersection Calculator
Conic Section Examples
-
Example 1: What will be the equation for the hyperbola which has center at (2, 3), vertex at (0, 3), and the focus at (5, 3).
Solution:
As we see, for hyperbola, all three points i.e., center, vertex, and focus lie on the same line y = 3.
Now we can see from the given points:
a = 2, c = 3
Hence
b2 = c2- a2 = 9 – 4 = 5.
Putting in the equation of hyperbola conic section:
(x−h)2/a2 - (y−k)2/b2 = 1
We get,
(x−2)2/22 - (y−3)2/5 = 1
Answer: Equation of the hyperbola will be (x−2)2/4 - (y−3)2/5 = 1.
-
Example 2: If for an ellipse, the focus lies at (3, 0), a vertex lies at (4, 0), and its center lies at (0, 0). Find the equation of the ellipse.
Solution:
From the given points, we can see that
c = 3 and a = 4.
Using b2 = a2 – c2
We get:
b2= 16 – 9 = 7
Putting in the equation of ellipse conic section:
x2/a2 + y2/b2 = 1
x2/16 + y2/7 = 1
Answer: The equation of the ellipse is x2/16 + y2/7 = 1.

FAQs on Conic Section
What Is Conic Section In Geometry?
A conic section is a geometric representation of a parabola, ellipse, hyperbola in a two-dimensional coordinate system. These conic are obtained from a simple cone and is obtained by cutting the cone across different sections.
What is Parabola in Conic Section?
When the intersecting plane is at an angle to the surface of the cone, we get a conic section named parabola. It is a U-shaped conic section. The value of eccentricity(e) for parabola is e = 1. It is a symmetrical open plane curve formed by the intersection of a cone with a plane parallel to its side. The path of a projectile under the influence of gravity ideally follows a curve of this shape.
The standard form of the equation of a parabola having the axis along the x-axis, and vertex at the origin is y2 = 4ax.
What is Circle in Conic Section?
The circle is a special type of ellipse where the cutting plane s parallel to the base of the cone. The circle has a focus known as the center of the circle. The locus of the points on the circle have a fixed distance from the focus or center of the circle and this fixed distance is called the radius of the circle. The value of eccentricity(e) for a circle is e = 0. Circle has no directrix. The general form of the equation of a circle with center at (h, k), and radius r, is as follows.
(x−h)2 + (y−k)2 = r2
What is Hyperbola in Conic Section?
A hyperbola is formed when the interesting plane is parallel to the axis of the cone, and intersect with both the nappes of the double cone. The hyperbola represents the locus of a point such that the difference of its distances from the two foci is a constant value. The eccentricity(e) for hyperbola has a value greater than 1. (e > 1)
The general form of the equation of the hyperbola with (h, k) as the center, the x-axis as the major axis, and the y-axis as the minor axis, is as follows.
(x−h)2/a2 - (y−k)2/b2 = 1
What is Ellipse in Conic Section?
Ellipse is a conic section that is formed when a plane intersects with the cone at an angle. Ellipse has 2 foci, a major axis, and a minor axis. Value of eccentricity(e) for ellipse is e < 1. Ellipse has 2 directrices. The general form of the equation of an ellipse with center at (h, k) and length of the major and minor axes as '2a' and '2b' respectively. The major axis of the ellipse is parallel to the x-axis.
(x−h)2/a2 + (y−k)2/b2 = 1
What is Eccentricity of a Conic Section?
The eccentricity of a conic section is the constant ratio of the distance of the point on the conic section from the focus and directrix. Eccentricity is used to uniquely define the shape of a conic section. It is a non-negative real number, which lies between 0 and 1. The excentricity values for the different conics is as follows.
- For circle, e = 0.
- For ellipse, 0 ≤ e < 1
- For parabola, e = 1
- For hyperbola, e > 1
What are the Applications of the Conic Section?
Here are a few real-life applications of conic sections which we might have seen or known are as follows.
- Planets travel around the Sun in elliptical routes at one focus.
- Mirrors used to direct light beams at the focus of the parabola are parabolic.
- Parabolic mirrors in solar ovens focus light beams for heating.
- Sound waves are focused on parabolic microphones.
- Car headlights and spotlights are designed based on parabola’s principles.
- The path traveled by objects thrown into the air is parabolic.
- Hyperbolas are used in long-range navigation systems called LORAN.
- Telescopes use parabolic mirrors.
visual curriculum