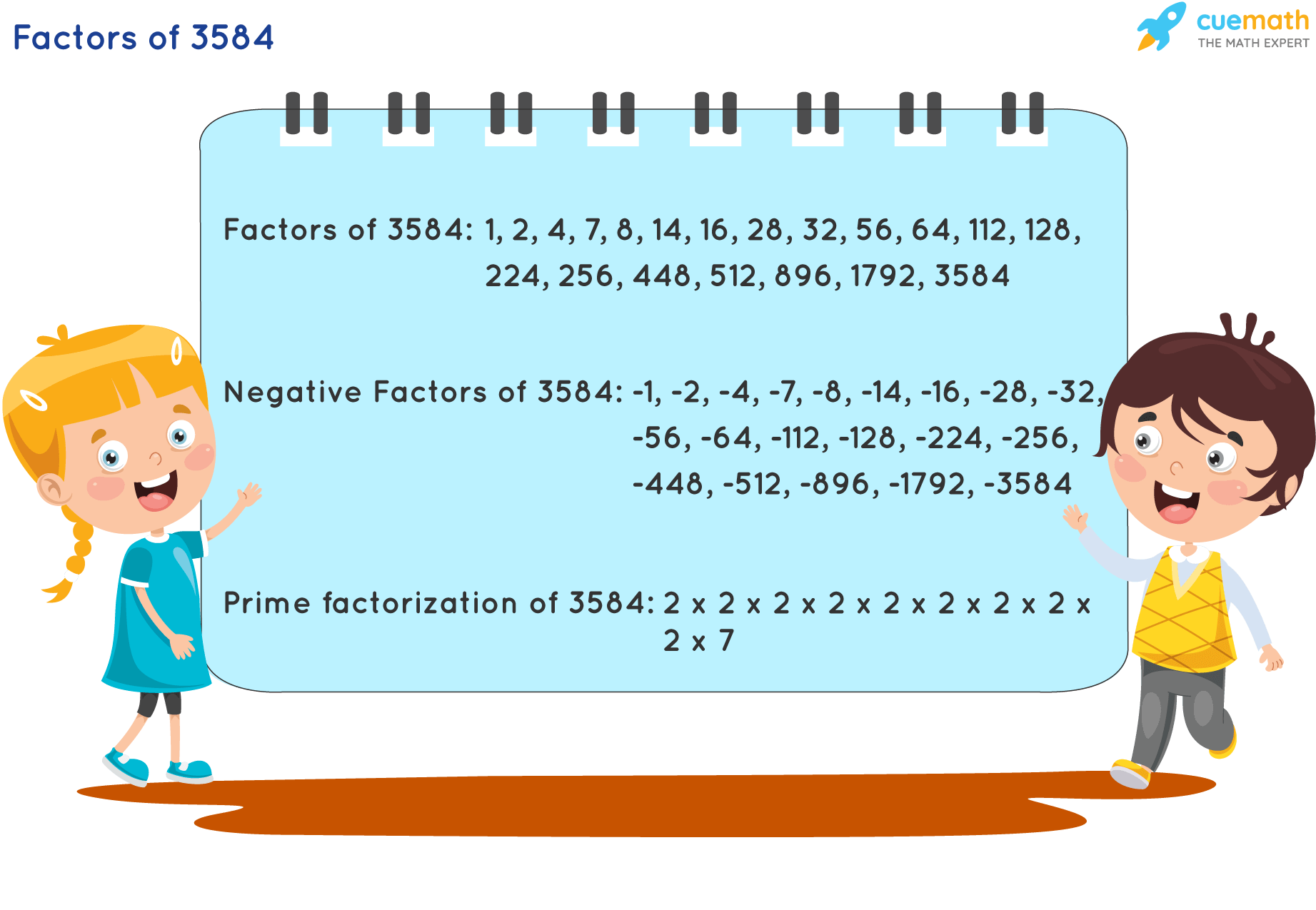
Factors of 3584 are the list of integers that can be evenly divided into 3584. There are total 20 factors of 3584, of which 2, 7 are its prime factors. The Prime Factorization of 3584 is 2⁹ × 7¹.

• All Factors of 3584: 1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 64, 112, 128, 224, 256, 448, 512, 896, 1792 and 3584
• Prime Factors of 3584: 2, 7
• Prime Factorization of 3584: 2⁹ × 7¹
• Sum of Factors of 3584: 8184

1.	What Are the Factors of 3584?
2.	Factors of 3584 by Prime Factorization
3.	Factors of 3584 in Pairs
4.	FAQs on Factors of 3584

Factors of 3584 are pairs of those numbers whose products result in 3584. These factors are either prime numbers or composite numbers.

How to Find the Factors of 3584?

To find the factors of 3584, we will have to find the list of numbers that would divide 3584 without leaving any remainder.

• 3584/64 = 56; therefore, 64 is a factor of 3584 and 56 is also a factor of 3584.
• 3584/7 = 512; therefore, 7 is a factor of 3584 and 512 is also a factor of 3584.

Similarly we can find other factors. Hence, the factors of 3584 are 1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 64, 112, 128, 224, 256, 448, 512, 896, 1792, 3584.

☛ Also Check:

• Factors of 27 - The factors of 27 are 1, 3, 9, 27
• Factors of 21 - The factors of 21 are 1, 3, 7, 21
• Factors of 50 - The factors of 50 are 1, 2, 5, 10, 25, 50
• Factors of 16 - The factors of 16 are 1, 2, 4, 8, 16
• Factors of 42 - The factors of 42 are 1, 2, 3, 6, 7, 14, 21, 42

The number 3584 is composite and therefore it will have prime factors. Now let us learn how to calculate the prime factors of 3584. The first step is to divide the number 3584 with the smallest prime factor, here it is 2. We keep dividing until it gives a non-zero remainder.

• 3584 ÷ 2 = 1792
• 1792 ÷ 2 = 896
• 896 ÷ 2 = 448
• 448 ÷ 2 = 224
• 224 ÷ 2 = 112
• 112 ÷ 2 = 56
• 56 ÷ 2 = 28
• 28 ÷ 2 = 14
• 14 ÷ 2 = 7

Further dividing 7 by 2 gives a non-zero remainder. So we stop the process and continue dividing the number 7 by the next smallest prime factor. We stop ultimately if the next prime factor doesn't exist or when we can't divide any further.

So, the prime factorization of 3584 can be written as 2⁹ × 7¹ where 2, 7 are prime.

Pair factors of 3584 are the pairs of numbers that when multiplied give the product 3584. The factors of 3584 in pairs are:

• 1 × 3584 = (1, 3584)
• 2 × 1792 = (2, 1792)
• 4 × 896 = (4, 896)
• 7 × 512 = (7, 512)
• 8 × 448 = (8, 448)
• 14 × 256 = (14, 256)
• 16 × 224 = (16, 224)
• 28 × 128 = (28, 128)
• 32 × 112 = (32, 112)
• 56 × 64 = (56, 64)

Negative pair factors of 3584 are:

• -1 × -3584 = (-1, -3584)
• -2 × -1792 = (-2, -1792)
• -4 × -896 = (-4, -896)
• -7 × -512 = (-7, -512)
• -8 × -448 = (-8, -448)
• -14 × -256 = (-14, -256)
• -16 × -224 = (-16, -224)
• -28 × -128 = (-28, -128)
• -32 × -112 = (-32, -112)
• -56 × -64 = (-56, -64)

NOTE: If (a, b) is a pair factor of a number then (b, a) is also a pair factor of that number.