Properties of Triangle
The properties of a triangle help us to identify a triangle from a given set of figures easily. A triangle is a polygon that has three angles, three sides, and three vertices. Triangles can be classified into different types of triangles based on the length of the sides and the measure of the angles. Let us learn more about the properties of triangles along with the theorems based on them.
| 1. | What are the Properties of Triangles? |
| 2. | Triangle and its Properties |
| 3. | FAQs on Properties of Triangles |
What are the Properties of Triangles?
In order to learn about the properties of triangles, we need to know about the different types of triangles. Although all triangles have some properties in common, there are a few properties that are based on their sides and angles.
Different Types of Triangles
Triangles can be classified into two broad categories based on their angles and sides. Observe the following figure which shows the types of triangles that are distinguished on the basis of their sides and angles.
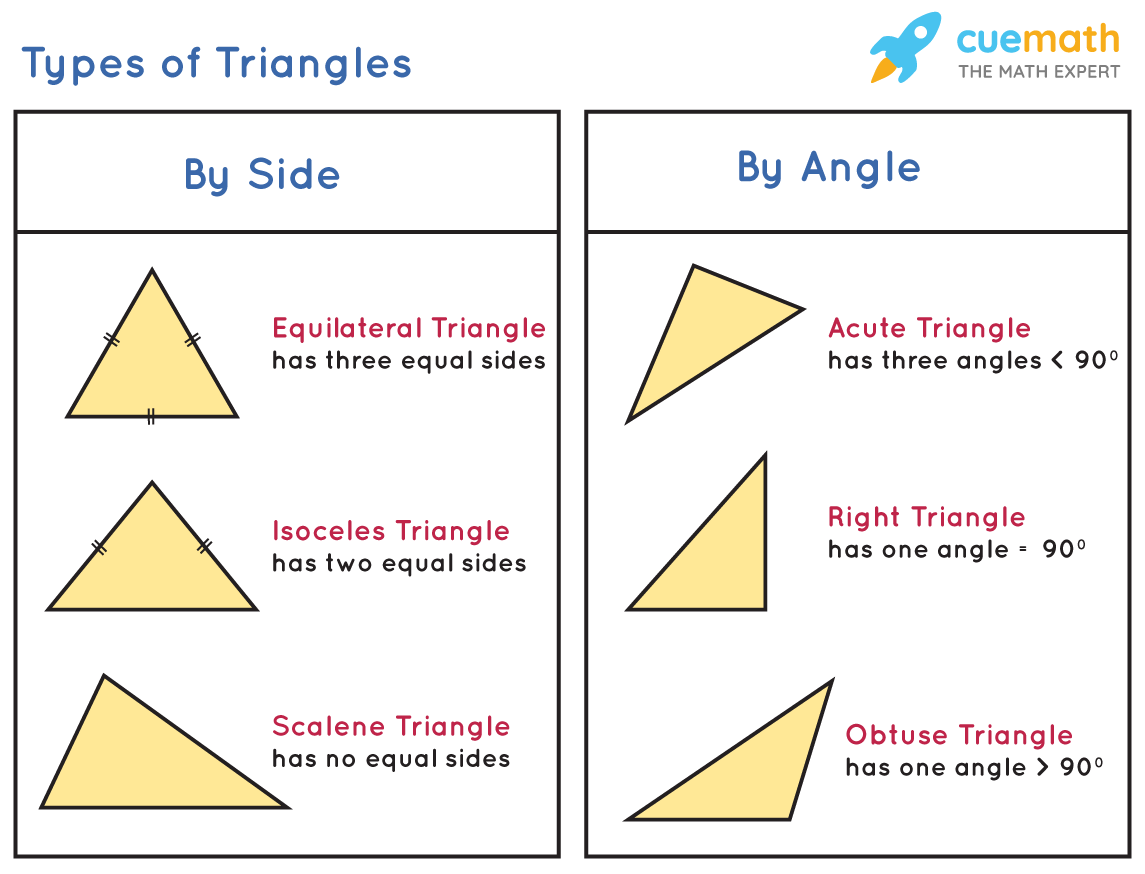
Triangle and its Properties
The properties of a triangle help us to identify relationships between different sides and angles of a triangle. Some of the important properties of a triangle are listed below.
Angle Sum Property
As per the angle sum property, the sum of the three interior angles of a triangle is always 180°.

In the given triangle, ∠P + ∠Q + ∠R = 180°
Triangle Inequality Property
As per the triangle inequality theorem, the sum of the length of the two sides of a triangle is greater than the third side.

Observe the figure given above which shows △ABC which represents the Triangle inequality property. If a = 4 units, b = 6 units, c = 3 units, let us verify the triangle inequality property as follows:
- a + b > c ( 4 + 6 > 3)
- c + a > b (3 + 4 > 6)
- c + b > a (3 + 6 > 4)
Pythagoras Property
As per the Pythagoras theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Mathematically, it can be expressed as Hypotenuse² = Base² + Altitude². Observe the figure given below to see the altitude, the base, and the hypotenuse.

Side Opposite the Greater Angle is the Longest Side
In order to understand this property which says that the side opposite the greater angle is the longest side, observe the triangle given below. In this triangle, ∠B is the greatest angle. Thus, the side AC is the longest side.

Exterior Angle Property
As per the exterior angle theorem, the exterior angle of a triangle is always equal to the sum of the interior opposite angles. In the given triangle, Exterior angle (e) = ∠a + ∠b
It should be noted that 3 exterior angles can be extended in a triangle and all these exterior angles add up to 360°.

Congruence Property
As per the Congruence Property, two triangles are said to be congruent if all their corresponding sides and angles are equal.

- ∠XYZ = ∠DEF
- ∠YXZ = ∠EDF
- ∠YZX = ∠EFD
- XY = DE
- XZ = DF
- YZ = EF
The basic triangle properties related to the area and perimeter of a triangle are given below.
- Area of a triangle: The total amount of space inside the triangle is called the area of a triangle. The area is measured in square units. The basic formula for calculating the area of a triangle is Area (A) = (1/2) × Base × Height
- Perimeter: The perimeter of a triangle = sum of all its three sides.
- Heron's formula: Heron’s formula is used to calculate the area of a triangle if the lengths of all the sides are known and the height of the triangle is not known. First, we need to calculate the semi-perimeter (s). For a triangle with sides a, b, and c, the semi-perimeter (s) = (a + b + c)/2, the area is given by; A = \(\sqrt{s(s-a)(s-b)(s-c)}\)
Important Notes
- The triangle is a polygon that has three angles, three sides, and three vertices.
- The sides and angles are very important aspects of a triangle. We can classify various types of triangles in math by combining sides and angles.
- The basic formula for calculating the area of a triangle is Area (A) = (1/2) × Base × Height
- The perimeter of a triangle is equal to the sum of all three sides of the triangle.
☛ Related Articles
Examples on Properties of Triangle
-
Example 1: Two angles of a triangle measure 75° and 60°. What will be the measure of its third angle?
Solution:
Measures of two angles of a triangle are 75° and 60°
Sum of the measures of two angles = 75° + 60° = 135°
Using the properties of a triangle, we know that the sum of all three angles of triangle = 180°
Therefore, the measure of the third angle = 180° - 135° = 45°.
-
Example 2: Tim wants to construct a triangle with the lengths of sides 5 cm, 4 cm, and 9 cm. Can he do it?
Solution:
The side lengths are 5 cm, 4 cm, 9 cm.
5 cm + 4 cm = 9 cm
Here the sum of the two smaller sides is equal to the third side. But as per the triangle inequality theorem, the sum of any two sides should be greater than the third side.
Hence, using the properties of the triangle we can say that Tim will not be able to construct a triangle with sides 5 cm, 4 cm, and 9 cm.
-
Example 3: The sides of a triangle are given as 3 cm, 4 cm, and 5 cm. Calculate the perimeter of the triangle.
Solution:
Sides of the triangle are: x = 3 cm, y = 4 cm and z = 5 cm
The perimeter of the triangle is given by P = x + y + zP = 3 + 4 + 5
P = 12 cm
Therefore, the perimeter of the given triangle is 12 cm.

FAQs on Properties of Triangle
What are the 5 Properties of a Triangle?
The basic properties of a triangle are listed below:
- A triangle has three sides, three vertices, and three angles.
- The sum of the three interior angles of a triangle is always 180°.
- The sum of the length of two sides of a triangle is always greater than the length of the third side.
- A triangle with vertices P, Q, and R is denoted as △PQR.
- The area of a triangle is equal to half of the product of its base and height.
How many Types of Triangles are there in Maths?
There are basically six types of triangles. They are scalene triangles, isosceles triangles, equilateral triangles, acute triangles, obtuse triangles, and right-angled triangles.
What is a Right-Angle Triangle?
A triangle that has one of the interior angles as 90 degrees is a right-angled triangle.
What do all Triangles have in Common?
Triangles come in different sizes and dimensions, however, there are some properties that all triangles have in common. For example, all triangles have three sides and three angles, the sum of the interior angles is always 180°, and the sum of the length of two sides of a triangle is always greater than the length of the third side.
What is the Area of a Triangle?
The area of a triangle is equal to half of the product of its base and height. It is the space enclosed by the sides of the triangle and is expressed with the formula, Area of triangle = 1/2 × base × height. The area of a triangle is expressed in square units.
What is the Triangle Inequality Theorem?
The Triangle inequality theorem states that the sum of the length of any two sides of a triangle is always greater than the length of the third side.
What are the Properties of a Scalene Triangle?
The properties of a scalene triangle are given as follows:
- It has three sides of different lengths.
- It has three angles of different measurements.
- It has no parallel or equal sides, hence, there is no line of symmetry.
- The interior angles of the triangle can be acute, obtuse, or right angles.
What are the Properties of a Right-angled Triangle?
The properties of a right-angled triangle are given as follows:
- The largest angle is always 90º which means it cannot have any obtuse angle.
- The largest side is called the hypotenuse which is always the side opposite to the right angle.
- The 3 sides of this triangle follow the Pythagoras theorem.
What are the Properties of an Isosceles Triangle?
The properties of an Isosceles triangle are given as follows:
- An isosceles triangle has two equal sides and the angle between them is called the vertex angle.
- The side that is opposite the vertex angle is called the base and base angles are equal.
- The perpendicular drawn from the vertex angle always bisects the base and the vertex angle.
What are the Properties of an Equilateral Triangle?
The properties of an equilateral triangle are given as follows:
- All the sides of an equilateral triangle are of equal length.
- All the angles of an equilateral triangle are equal to 60°.
- If a perpendicular is drawn from any of the vertices to the opposite side, it bisects that side and also bisects the vertex angle.
- The orthocenter and centroid of an equilateral triangle fall at the same point.
What is the Angle Sum Property of a Triangle?
According to the Angle sum property of a triangle, the sum of the interior angles of a triangle is always 180°. For example, if the 3 interior angles of a triangle are given as ∠a, ∠b, and ∠c, then this property can be expressed as, ∠a + ∠b + ∠c = 180°.
visual curriculum