A day full of math games & activities. Find one near you.

Cot pi/2

The value of cot pi/2 is 0. Cot pi/2 radians in degrees is written as cot ((π/2) × 180°/π), i.e., cot (90°). In this article, we will discuss the methods to find the value of cot pi/2 with examples.

Cot pi/2: 0
Cot (-pi/2): 0
Cot pi/2 in degrees: cot (90°)

What is the Value of Cot pi/2?

The value of cot pi/2 is 0. Cot pi/2 can also be expressed using the equivalent of the given angle (pi/2) in degrees (90°).

We know, using radian to degree conversion, θ in degrees = θ in radians × (180°/pi)
⇒ pi/2 radians = pi/2 × (180°/pi) = 90° or 90 degrees
∴ cot pi/2 = cot π/2 = cot(90°) = 0

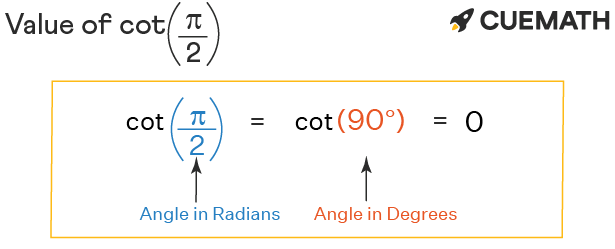
Explanation:

For cot pi/2, the angle pi/2 lies on the positive y-axis. Thus, cot pi/2 value = 0
Since the cotangent function is a periodic function, we can represent cot pi/2 as, cot pi/2 = cot(pi/2 + n × pi), n ∈ Z.
⇒ cot pi/2 = cot 3pi/2 = cot 5pi/2 , and so on.
Note: Since, cotangent is an odd function, the value of cot(-pi/2) = -cot(pi/2) = 0.

Methods to Find Value of Cot pi/2

The value of cot pi/2 is given as 0. We can find the value of cot pi/2 by:

Using Unit Circle
Using Trigonometric Functions

Cot pi/2 Using Unit Circle

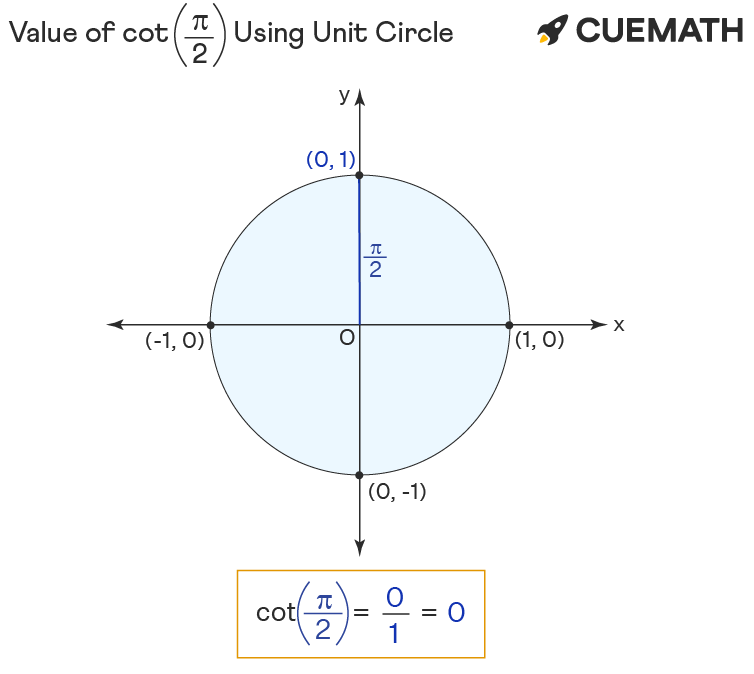
To find the value of cot π/2 using the unit circle:

Rotate ‘r’ anticlockwise to form pi/2 angle with the positive x-axis.
The cot of pi/2 equals the x-coordinate(0) divided by y-coordinate(1) of the point of intersection (0, 1) of unit circle and r.

Hence the value of cot pi/2 = x/y = 0

Cot pi/2 in Terms of Trigonometric Functions

Using trigonometry formulas, we can represent the cot pi/2 as:

cos(pi/2)/sin(pi/2)
± cos(pi/2)/√(1 - cos²(pi/2))
± √(1 - sin²(pi/2))/sin(pi/2)
± 1/√(sec²(pi/2) - 1)
± √(cosec²(pi/2) - 1)
1/tan(pi/2)

Note: Since pi/2 lies on the positive y-axis, the final value of cot pi/2 is 0.

We can use trigonometric identities to represent cot pi/2 as,

tan (pi/2 - pi/2) = tan 0
-tan (pi/2 + pi/2) = -tan pi
-cot (pi - pi/2) = -cot pi/2

☛ Also Check:

Examples Using Cot pi/2

Example 1: Using the value of cot pi/2, solve: (cosec²(pi/2) - 1).

Solution:
We know, (cosec²(pi/2) - 1) = (cot²(pi/2)) = 0
⇒ (cosec²(pi/2) - 1) = 0
Example 2: Find the value of 9 cot(pi/2)/10 cot(pi/4).

Solution:

Using trigonometric values, we know, cot(pi/2) = 0 and cot(pi/4) = 1.
⇒ Value of 9 cot(pi/2)/10 cot(pi/4) = 0
Example 3: Simplify: 5 (cot(pi/2)/tan(pi/4))

Solution:

We know cot pi/2 = 0 and tan pi/4 = 1
⇒ 5 cot(pi/2)/tan(pi/4) = 0

go to slide go to slide go to slide

Ready to see the world through math’s eyes?

Math is at the core of everything we do. Enjoy solving real-world math problems in live classes and become an expert at everything.

Book a Free Trial Class

FAQs on Cot pi/2

What is Cot pi/2?

Cot pi/2 is the value of cotangent trigonometric function for an angle equal to π/2 radians. The value of cot pi/2 is 0.

How to Find Cot pi/2 in Terms of Other Trigonometric Functions?

Using trigonometry formula, the value of cot pi/2 can be given in terms of other trigonometric functions as:

cos(pi/2)/sin(pi/2)
± cos(pi/2)/√(1 - cos²(pi/2))
± √(1 - sin²(pi/2))/sin(pi/2)
± 1/√(sec²(pi/2) - 1)
± √(cosec²(pi/2) - 1)
1/tan(pi/2)

☛ Also check: trigonometry table

What is the Value of Cot pi/2 in Terms of Cos pi/2?

We know, using trig identities, we can write cot pi/2 as cos(pi/2)/√(1 - cos²(pi/2)). Here, the value of cos pi/2 is equal to 0.

How to Find the Value of Cot pi/2?

The value of cot pi/2 can be calculated by constructing an angle of π/2 radians with the x-axis, and then finding the coordinates of the corresponding point (0, 1) on the unit circle. The value of cot pi/2 is equal to the x-coordinate(0) divided by the y-coordinate (1). ∴ cot pi/2 = 0

What is the Value of Cot pi/2 in Terms of Cosec pi/2?

Since the cotangent function can be represented using the cosecant function, we can write cot pi/2 as √(cosec²(pi/2) - 1). The value of cosec pi/2 is equal to 1.

Download FREE Study Materials

Trigonometry

Math worksheets and
visual curriculum