Square Root of 66
The number 66 is an even composite number with three prime factors, i.e., 2, 3, and 11. The square root of a number implies a number which when multiplied with itself results in the given number. The square root of 66 can be a rational or irrational number. We will now look at different methods to find the value of the square root of 66 and look at some interesting problems as well.
- Square root of 66: √66 = 8.1240
- Square of 66: (66)2 = 4356
| 1. | What Is the Square Root of 66? |
| 2. | Is Square Root of 66 Rational or Irrational? |
| 3. | How to Find the Square Root of 66? |
| 4. | FAQs on Square Root of 66 |
| 5. | Important Notes on Square Root of 66 |
What Is the Square Root of 66?
- The square root of 66 is written as √66 (radical form) = 8.1240
- The square root of 66 can be written as (66)1/2 in exponential form.
- The number 66 has three prime factors, i.e., 2, 3, and 11 with their power equal to 1. So, the square root of 66 cannot be simplified further using prime factorization.
Is Square Root of 66 Rational or Irrational?
The square root of 66 is a non-repeating and non-terminating number. Therefore, it cannot be written in the form of p/q where q ≠ 0.
Hence, the square root of 66 is an irrational number.
How to Find the Square Root of 66?
We will now find the square root of 66 using the following methods:
- Approximation Method
- Long Division Method
Square Root of 66 Using Approximation Method
- We will find two consecutive perfect squares such that 66 lies between them. The two perfect squares are 64 (82) and 81 (92).
So, the whole number part of the square root of 66 will be 8. - Now, for the decimal part, we will use the formula:
(Given number - Smaller perfect square) / (Greater perfect square - Smaller perfect square)
= (66 - 64)/(81 - 64) = 2/17 = 0.117 - Hence, the square root of 66 by approximation method is 8.117
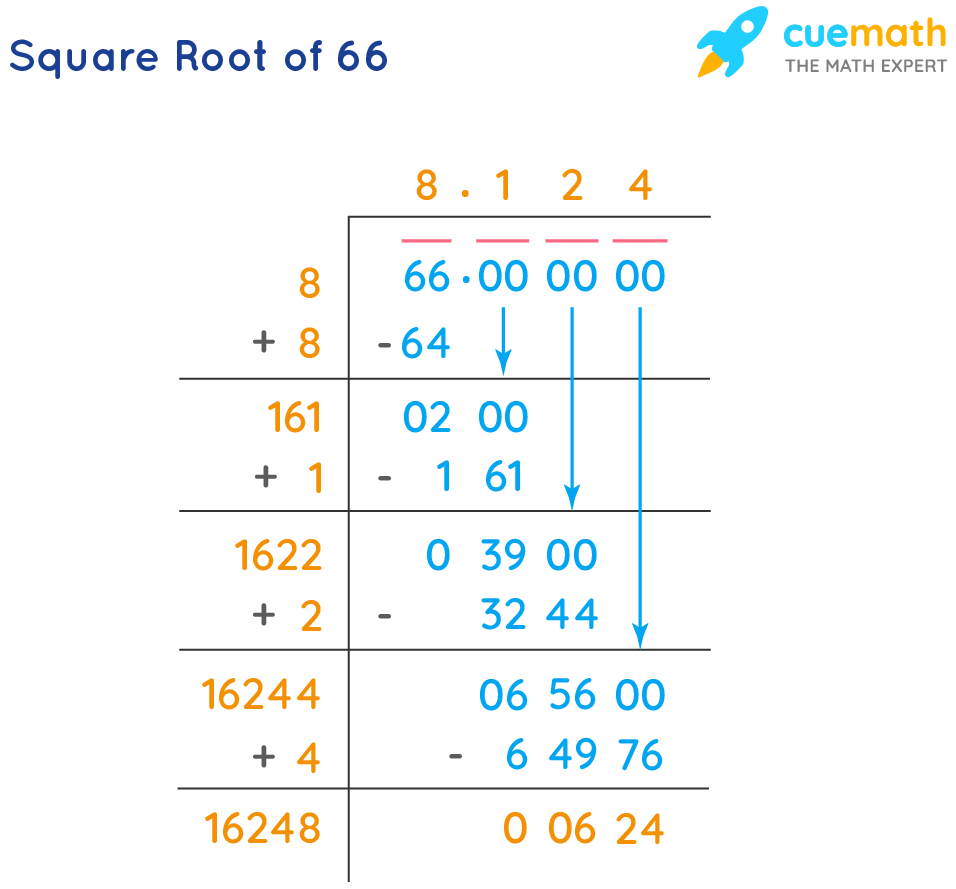
Square Root of 66 by Long Division
Now we will calculate the square root of 66 by the long division method.
- Start pairing the digits by adding a bar on top of them from the unit’s place. We will have only one pair in the case of 66.
- Find a number(b) such that b × b ≤ 66. So, b will be 8 as 8 × 8 = 64.
- We get the remainder as 2 (66-64) and the quotient as 8. Now, we will add the divisor b with itself (b + b) and get the new divisor (16).
- Put a decimal in the dividend and quotient simultaneously. Also, place 3 pairs of zero in the dividend part after the decimal (66.00 00 00).
- Bring down one pair of zeros. So, our new dividend is 200. Find a number(n) such that 16n × n ≤ 200. The number m will be 1 as 161 × 1 = 161 ≤ 200.
- Repeat the above step for the remaining pairs of zeros.
So, we get the square root of √66 = 8.124 by the long division method.
Explore square roots using illustrations and interactive examples.
Important Notes:
- The number 66 is not a perfect square.
- The square root of 66 is an irrational number.
- The square root of -66 is an imaginary number.
Square Root of 66 Solved Examples
-
Example 1: What is the % error in the square root of 66 calculated via the approximation method. Also, tell whether it is underestimated or overestimated?
Solution:
The actual square root of 66 = 8.1240
The estimated square root of 66 = 8.117
Hence, it is underestimated.
Now % error = ((8.1240 - 8.117)/8.1240) × 100 = 0.086% -
Example 2: Mike wants to coat his square-shaped table with a surface area of √66 square feet. The cost of coating is $15 per square feet. How much will he have to pay?
Solution:
Surface area of table = √66 = 8.124 square feet
Cost of coating 1 square feet = $15
Therefore, cost of coating 8.124 square feet = 8.124 × 15 = $121.86

FAQs on Square Roots of 66
What is the negative square root of 66?
The negative square root of 66 is -8.1240.
Is the square root of 66 is a rational number?
No, the square root of 66 is not a rational number.
It's because it cannot be expressed in the form of p/q where q ≠ 0.
Is the number 66 a perfect square?
No, the number 66 is not a perfect square.
The square root of 66 is an irrational number and all perfect squares have integers as their square root.
Can we find the square root of 66 using the repeated subtraction method?
No, we can’t find the square root of 66 via the repeated subtraction method.
It's because the number 66 is not a perfect square.
What is the square root of -66?
The square root of all negative numbers are imaginary numbers.
So, the square of -66 is represented as √-66 = ±8.124i. (where i = √-1)
visual curriculum