LCM of 3 and 17
LCM of 3 and 17 is the smallest number among all common multiples of 3 and 17. The first few multiples of 3 and 17 are (3, 6, 9, 12, 15, 18, . . . ) and (17, 34, 51, 68, 85, 102, . . . ) respectively. There are 3 commonly used methods to find LCM of 3 and 17 - by division method, by prime factorization, and by listing multiples.
| 1. | LCM of 3 and 17 |
| 2. | List of Methods |
| 3. | Solved Examples |
| 4. | FAQs |
What is the LCM of 3 and 17?
Answer: LCM of 3 and 17 is 51.
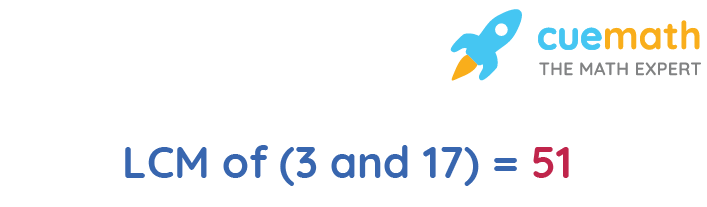
Explanation:
The LCM of two non-zero integers, x(3) and y(17), is the smallest positive integer m(51) that is divisible by both x(3) and y(17) without any remainder.
Methods to Find LCM of 3 and 17
The methods to find the LCM of 3 and 17 are explained below.
- By Listing Multiples
- By Division Method
- By Prime Factorization Method
LCM of 3 and 17 by Listing Multiples
To calculate the LCM of 3 and 17 by listing out the common multiples, we can follow the given below steps:
- Step 1: List a few multiples of 3 (3, 6, 9, 12, 15, 18, . . . ) and 17 (17, 34, 51, 68, 85, 102, . . . . )
- Step 2: The common multiples from the multiples of 3 and 17 are 51, 102, . . .
- Step 3: The smallest common multiple of 3 and 17 is 51.
∴ The least common multiple of 3 and 17 = 51.
LCM of 3 and 17 by Division Method
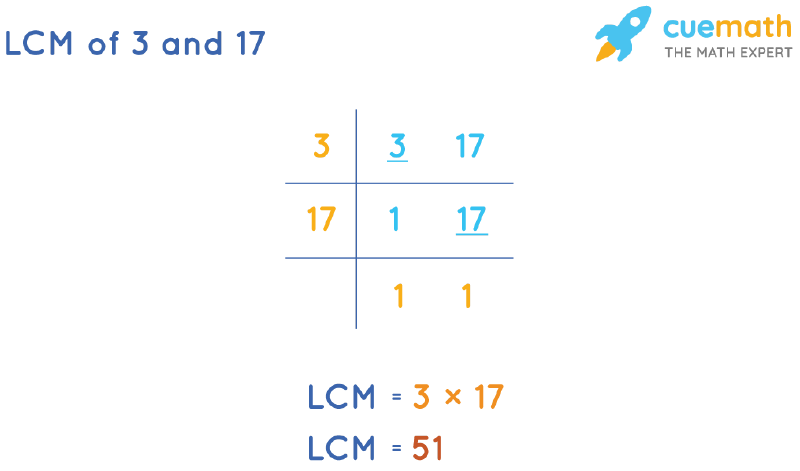
To calculate the LCM of 3 and 17 by the division method, we will divide the numbers(3, 17) by their prime factors (preferably common). The product of these divisors gives the LCM of 3 and 17.
- Step 1: Find the smallest prime number that is a factor of at least one of the numbers, 3 and 17. Write this prime number(3) on the left of the given numbers(3 and 17), separated as per the ladder arrangement.
- Step 2: If any of the given numbers (3, 17) is a multiple of 3, divide it by 3 and write the quotient below it. Bring down any number that is not divisible by the prime number.
- Step 3: Continue the steps until only 1s are left in the last row.
The LCM of 3 and 17 is the product of all prime numbers on the left, i.e. LCM(3, 17) by division method = 3 × 17 = 51.
LCM of 3 and 17 by Prime Factorization
Prime factorization of 3 and 17 is (3) = 31 and (17) = 171 respectively. LCM of 3 and 17 can be obtained by multiplying prime factors raised to their respective highest power, i.e. 31 × 171 = 51.
Hence, the LCM of 3 and 17 by prime factorization is 51.
☛ Also Check:
- LCM of 9 and 24 - 72
- LCM of 35 and 49 - 245
- LCM of 60 and 90 - 180
- LCM of 14 and 18 - 126
- LCM of 9 and 27 - 27
- LCM of 12, 15 and 45 - 180
- LCM of 3, 9 and 18 - 18
LCM of 3 and 17 Examples
-
Example 1: The GCD and LCM of two numbers are 1 and 51 respectively. If one number is 17, find the other number.
Solution:
Let the other number be p.
∵ GCD × LCM = 17 × p
⇒ p = (GCD × LCM)/17
⇒ p = (1 × 51)/17
⇒ p = 3
Therefore, the other number is 3. -
Example 2: Verify the relationship between GCF and LCM of 3 and 17.
Solution:
The relation between GCF and LCM of 3 and 17 is given as,
LCM(3, 17) × GCF(3, 17) = Product of 3, 17
Prime factorization of 3 and 17 is given as, 3 = (3) = 31 and 17 = (17) = 171
LCM(3, 17) = 51
GCF(3, 17) = 1
LHS = LCM(3, 17) × GCF(3, 17) = 51 × 1 = 51
RHS = Product of 3, 17 = 3 × 17 = 51
⇒ LHS = RHS = 51
Hence, verified. -
Example 3: Find the smallest number that is divisible by 3 and 17 exactly.
Solution:
The value of LCM(3, 17) will be the smallest number that is exactly divisible by 3 and 17.
⇒ Multiples of 3 and 17:- Multiples of 3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, . . . ., 45, 48, 51, . . . .
- Multiples of 17 = 17, 34, 51, 68, 85, 102, 119, 136, 153, 170, . . . ., 17, 34, 51, . . . .
Therefore, the LCM of 3 and 17 is 51.

FAQs on LCM of 3 and 17
What is the LCM of 3 and 17?
The LCM of 3 and 17 is 51. To find the LCM (least common multiple) of 3 and 17, we need to find the multiples of 3 and 17 (multiples of 3 = 3, 6, 9, 12 . . . . 51; multiples of 17 = 17, 34, 51, 68) and choose the smallest multiple that is exactly divisible by 3 and 17, i.e., 51.
What are the Methods to Find LCM of 3 and 17?
The commonly used methods to find the LCM of 3 and 17 are:
- Listing Multiples
- Division Method
- Prime Factorization Method
How to Find the LCM of 3 and 17 by Prime Factorization?
To find the LCM of 3 and 17 using prime factorization, we will find the prime factors, (3 = 3) and (17 = 17). LCM of 3 and 17 is the product of prime factors raised to their respective highest exponent among the numbers 3 and 17.
⇒ LCM of 3, 17 = 31 × 171 = 51.
If the LCM of 17 and 3 is 51, Find its GCF.
LCM(17, 3) × GCF(17, 3) = 17 × 3
Since the LCM of 17 and 3 = 51
⇒ 51 × GCF(17, 3) = 51
Therefore, the GCF = 51/51 = 1.
What is the Relation Between GCF and LCM of 3, 17?
The following equation can be used to express the relation between GCF and LCM of 3 and 17, i.e. GCF × LCM = 3 × 17.
visual curriculum