Properties of Integers
The properties of integers make calculations easier and faster. Integers are a set of numbers that include natural numbers, zero, and negative numbers. They do not have any fractional parts. Let us learn about the properties of integers in this article.
What are the Properties of Integers?
The following points show the list of the various properties of integers:
- Closure Property
- Associative Property
- Commutative Property
- Distributive Property
- Identity Property
These properties are applicable to whole numbers, natural numbers, rational numbers, and real numbers. Observe the figure given below to have an overview of the applicability of different properties of integers on the four basic arithmetic operations on integers. A detailed explanation of each of the properties is given in the sections below.
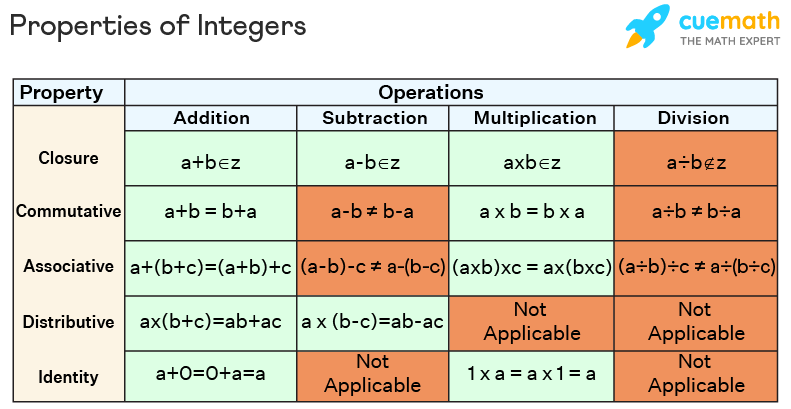
Closure Property of Integers
The closure property of integers states that the addition, subtraction, and multiplication of two integers always results in an integer. So, this implies if {a, b} ∈ Z, then c ∈ Z, such that
- a + b = c
- a - b = c
- a × b = c
The closure property of integers does not hold true for the division of integers as the division of two integers may not always result in an integer. For example, we know that 3 and 4 are integers but 3 ÷ 4 = 0.75 which is not an integer. Therefore, the closure property is not applicable to the division of integers. It holds true for the addition, subtraction, and multiplication of integers. Let us look at some examples of closure property of integers given below:
- -2 + 7 = 5, where {-2, 5, 7} ∈ Z.
- -9 - (-8) = -1, where {-9, -8, -1} ∈ Z.
- -7 × 0 = 0, where {-7, 0} ∈ Z.
Associative Property of Integers
The associative property of integers under addition and multiplication states that the result of the addition and multiplication of more than two integers is always the same irrespective of the grouping of integers. This implies that for any three integers a, b, and c, we have,
- a + (b + c) = (a + b) + c = (a + c) + b
- a × (b × c) = (a × b) × c = (a × c) × b
The associative property of integers does not hold true for subtraction and division of integers, as, in the case of subtraction and division, the order of the numbers is important and cannot be changed. For example, 2 - (8 - 9) = 2 - (-1) = 3. Now, if we change the order as 8 - (2 - 9) = 8 - (-7) = 15. Therefore, 2 - (8 - 9) ≠ 8 - (2 - 9). The examples of associative property of integers are given in the table below:
| Operation | Example | Result |
| Addition | - 8 + (4 + 2) = (-8 + 4) + 2 = -2 | Satisfied |
| Subtraction |
- 8 - (4 - 2) = -8 - 2 = -10 (-8 - 4) - 2 = - 12 - 2 = -14 |
Does not hold true |
| Multiplication | - 8 × (4 × 2) = (-8 × 4) × 2 = - 64 | Satisfied |
| Division |
- 8 ÷ (4 ÷ 2) = -4 (-8 ÷ 4) ÷ 2 = -1 |
Does not hold true |
Commutative Property of Integers
The commutative property of integers is similar to the associative property; the only difference is that in this property, we take only two integers. The commutative property of integers under addition and multiplication states that the result of the addition and multiplication of two integers is always the same regardless of their order. This implies, if there are two integers a and b, we have,
- a + b = b + a
- a × b = b × a
This property does not hold true with subtraction and division operations. Let us look at the examples of the commutative property of integers under addition, subtraction, multiplication, and division.
| Operation | Examples | Result |
| Addition | -6 + 3 = 3 + (-6) = -3 | Satisfied |
| Subtraction |
-6 - 3 = -9 3 - (-6) = 9 |
Does not hold true |
| Multiplication | -6 × 3 = 3 × (-6) = -18 | Satisfied |
| Division |
-6 ÷ 3 = -2 3 ÷ (-6) = -1/2 |
Does not hold true |
Distributive Property of Integers
The distributive property of integers states that the multiplication operation can be distributed over addition and subtraction to make calculations easier. This implies, for any three integers, a, b, and c, we have,
- a × (b + c) = (a × b) + (a × c)
- a × (b - c) = (a × b) - (a × c)
This property has many applications in math. We can use it for mental calculations. For example, what is the value of -6 × 98? This can be written as -6 × (100 - 2). Now we can apply the distributive property of integers on this to get (-6 × 100) - (-6 × 2) = -600 - (-12) = - 600 + 12 = -588.
Identity Property of Integers
The identity property of the addition of integers states that any number added to 0 results in the same number. For an instance, if 'a' is any integer, this implies, a + 0 = 0 + a = a. Let us take an example of a negative integer -5. If we add 0 to -5, we will get -5. There is no change in the result. So, we can say that 0 is the identity element of the addition of integers.
In the case of multiplication of integers, can you think of any number which we can multiply with an integer to get the same integer as the product? Yes, the multiplicative identity element for integers is 1. We can multiply 1 to any integer to get the same result. For example, a × 1 = 1 × a = a.
The identity property of integers does not hold true for subtraction and division operations. In the case of subtraction, if we subtract any number from 0, we will get its additive inverse. So, if 'p' is any integer, then p - 0 = p, but 0 - p = -p. In the case of division of integers, if 'm' is any integer, then m ÷ 1 = m, but 1 ÷ m ≠ m. Therefore, there is no identity element for subtraction and division of integers.
☛ Related Articles
Properties of Integers Examples
-
Example 1: Evaluate the expression: (-20 × 15) + (-20 × 18) using the properties of integers.
Solution: The given expression is (-20 × 15) + (-20 × 18). It can be solved by using the distributive property of integers, which states (a × b) + (a × c) = a × (b + c). So, here we can take (-20) as common out of both the terms. We get -20 × (15 + 18).
⇒ - 20 × 33
= - 660
Therefore, (-20 × 15) + (-20 × 18) = -660.
-
Example 2: Olivia has recently learned about the properties of integers. She believed that 0 is the identity element for the subtraction of integers as well as we can subtract 0 from any integer to get the same integer as the answer. Is she right? State the reason.
Solution: 0 is not the identity element for subtraction. So, Olivia is not right. Let us look at the reason. It is true that if we subtract 0 from any integer, we get the same integer as the answer. But to make it an identity element, its reverse should also be true. If we subtract any number from 0, we get its additive inverse. This implies, if 'a' is any integer, then a - 0 = a, but 0 - a = -a. Therefore, 0 is not the identity element for subtraction.
-
Example 3: Identify the correct properties of integers in the following:
a.) a + b = b + a
b.) a × (b - c) = (a × b) - (a × c)
Solution:
a.) a + b = b + a shows the Commutative property of integers.
b.) a × (b - c) = (a × b) - (a × c) shows the Distributive property of integers.

FAQs on Properties of Integers
What are the Properties of Integers?
Properties of integers are a set of basic rules that make our calculations easier and provide a reason for various operations on integers. For example, the Identity property of addition of integers states that any number added to 0 results in the same number. In other words, a + 0 = 0 + a = a. Similarly, there are other properties of integers that are useful in solving bigger expressions.
What is the Importance of Knowing the Properties of Integers?
The importance of knowing the properties of integers is that it makes our calculations easier. We can easily solve any equation based on the operations of integers if we know their properties. For example, by using the commutative law, it becomes easy for us to add -24 to 2. As we can do it in any of the ways, either -24 + 2 or 2 + (-24).
What are the Properties of Integers under Multiplication?
The properties of integers under multiplication are given below:
- Multiplying 1 with any integer results in the same number.
- 0 multiplied to any integer always results in 0.
- Closure property
- Associative property
- Multiplication is distributive over addition and subtraction
- Commutative property
What are the Properties of Division of Integers?
The properties of integers division are given below:
- Dividing any integer by 1 results in the same integer.
- 0 divided by any integer is always 0.
- 0 divided by 0 is not defined.
- Division of integers does not always satisfy the closure property, the associative property, and the commutative property.
What are the Properties of Integers under Addition?
The properties of integers under addition are given below:
- The addition of two integers satisfies the closure property.
- Two or more integers can be added in any order.
- 0 added to any integer does not change its value.
What are the Four Properties of Integers?
The four commonly used properties of integers are the closure property, the commutative property, the associative property, and the distributive property.
visual curriculum