Sin 9pi/4
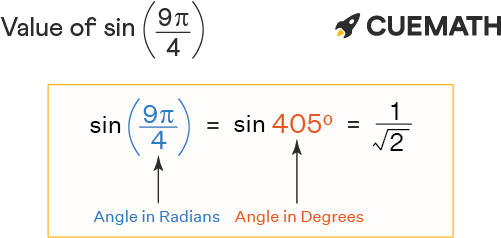
The value of sin 9pi/4 is 0.7071067. . .. Sin 9pi/4 radians in degrees is written as sin ((9π/4) × 180°/π), i.e., sin (405°). In this article, we will discuss the methods to find the value of sin 9pi/4 with examples.
- Sin 9pi/4: 1/√2
- Sin 9pi/4 in decimal: 0.7071067. . .
- Sin (-9pi/4): -0.7071067. . . or -(1/√2)
- Sin 9pi/4 in degrees: sin (405°)
What is the Value of Sin 9pi/4?
The value of sin 9pi/4 in decimal is 0.707106781. . .. Sin 9pi/4 can also be expressed using the equivalent of the given angle (9pi/4) in degrees (405°).
We know, using radian to degree conversion, θ in degrees = θ in radians × (180°/pi)
⇒ 9pi/4 radians = 9pi/4 × (180°/pi) = 405° or 405 degrees
∴ sin 9pi/4 = sin 9π/4 = sin(405°) = 1/√2 or 0.7071067. . .
Explanation:
For sin 9pi/4, the angle 9pi/4 > 2pi. Given the periodic property of the sine function, we can represent it as sin(9pi/4 mod 2pi) = sin(pi/4). The angle 9pi/4, coterminal to angle pi/4, is located in the First Quadrant(Quadrant I).
Since sin function is positive in the 1st quadrant, thus sin 9pi/4 value = 1/√2 or 0.7071067. . .
Similarly, sin 9pi/4 can also be written as, sin 9pi/4 = (9pi/4 + n × 2pi), n ∈ Z.
⇒ sin 9pi/4 = sin 17pi/4 = sin 25pi/4, and so on.
Note: Since, sine is an odd function, the value of sin(-9pi/4) = -sin(9pi/4).
Methods to Find Value of Sin 9pi/4
The sine function is positive in the 1st quadrant. The value of sin 9pi/4 is given as 0.70710. . .. We can find the value of sin 9pi/4 by:
- Using Unit Circle
- Using Trigonometric Functions
Sin 9pi/4 Using Unit Circle
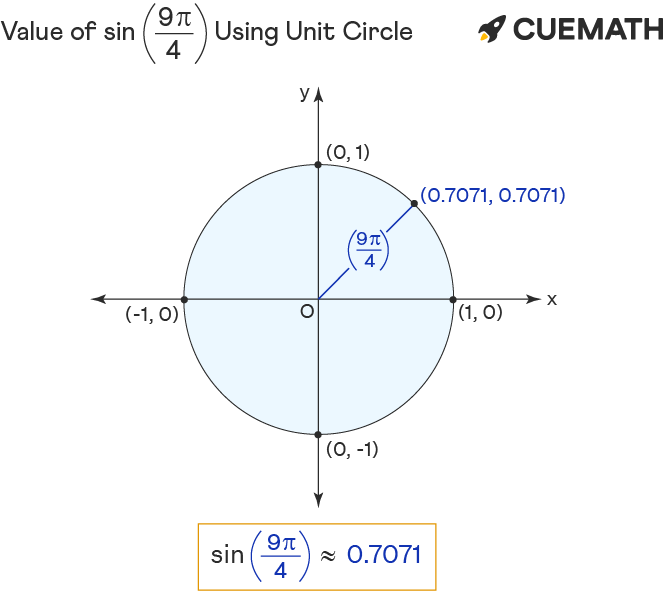
To find the value of sin 9π/4 using the unit circle, represent 9pi/4 in the form (1 × 2pi) + pi/4 [∵ 9pi/4>2pi] ∵ sine is a periodic function, sin 9pi/4 = sin pi/4.
- Rotate ‘r’ anticlockwise to form pi/4 or 9pi/4 angle with the positive x-axis.
- The sin of 9pi/4 equals the y-coordinate(0.7071) of the point of intersection (0.7071, 0.7071) of unit circle and r.
Hence the value of sin 9pi/4 = y = 0.7071 (approx)
Sin 9pi/4 in Terms of Trigonometric Functions
Using trigonometry formulas, we can represent the sin 9pi/4 as:
- ± √(1-cos²(9pi/4))
- ± tan(9pi/4)/√(1 + tan²(9pi/4))
- ± 1/√(1 + cot²(9pi/4))
- ± √(sec²(9pi/4) - 1)/sec(9pi/4)
- 1/cosec(9pi/4)
Note: Since 9pi/4 lies in the 1st Quadrant, the final value of sin 9pi/4 will be positive.
We can use trigonometric identities to represent sin 9pi/4 as,
- sin(pi - 9pi/4) = sin(-5pi/4)
- -sin(pi + 9pi/4) = -sin 13pi/4
- cos(pi/2 - 9pi/4) = cos(-7pi/4)
- -cos(pi/2 + 9pi/4) = -cos 11pi/4
☛ Also Check:
FAQs on Sin 9pi/4
What is Sin 9pi/4?
Sin 9pi/4 is the value of sine trigonometric function for an angle equal to 9pi/4 radians. The value of sin 9pi/4 is 1/√2 or 0.7071 (approx).
How to Find Sin 9pi/4 in Terms of Other Trigonometric Functions?
Using trigonometry formula, the value of sin 9π/4 can be given in terms of other trigonometric functions as:
- ± √(1-cos²(9pi/4))
- ± tan(9pi/4)/√(1 + tan²(9pi/4))
- ± 1/√(1 + cot²(9pi/4))
- ± √(sec²(9pi/4) - 1)/sec(9pi/4)
- 1/cosec(9pi/4)
☛ Also check: trigonometry table
What is the Value of Sin 9pi/4 in Terms of Sec 9pi/4?
Since the sine function can be represented using the secant function, we can write sin 9pi/4 as √(sec²(9pi/4) - 1)/sec 9pi/4. The value of sec 9pi/4 is equal to 1.414213.
What is the Value of Sin 9pi/4 in Terms of Tan 9pi/4?
We know, using trig identities, we can write sin 9pi/4 as tan(9pi/4)/√(1 + tan²(9pi/4)). Here, the value of tan 9pi/4 is equal to 1.
How to Find the Value of Sin 9pi/4?
The value of sin 9pi/4 can be calculated by constructing an angle of 9π/4 radians with the x-axis, and then finding the coordinates of the corresponding point (0.7071, 0.7071) on the unit circle. The value of sin 9pi/4 is equal to the y-coordinate (0.7071). ∴ sin 9pi/4 = 0.7071.