Adding Integers
Adding integers is the process of finding the sum of two or more integers. It may result in an increase or a decrease in value, depending on whether the integers are positive or negative or a mixture. The addition of integers is an arithmetic operation performed on integers with the same sign or with different signs to find the sum. Let us learn more about adding integers in this article.
| 1. | Rules for Addition of Integers |
| 2. | Adding Integers on a Number Line |
| 3. | FAQs on Adding Integers |
Rules for Addition of Integers
There are certain rules to be followed to add two or more integers. Integers are complete numbers that do not have fractional parts. It includes positive integers, zero, and negative integers.
How to Add Integers?
The rules for adding integers are given below:
- The sum of an integer and its additive inverse is 0. For example, 4 + (-4) = 0
- Adding two positive integers always results in a positive value. For example, 6 + 6 = 12
- Adding two negative integers always results in a negative number. For example, (-6) + (-6) = -12
- Adding integers with 0 results in the same number. For example, 6 + 0 = 6, and -8 + 0 = -8
- Adding a positive number with a negative number is done by finding the difference between the absolute value of both numbers. Then, the sign with the greater number gets attached to the sum. For example, +7 - 3 = +4
The rules for the addition of integers can be understood with the help of the table given below.
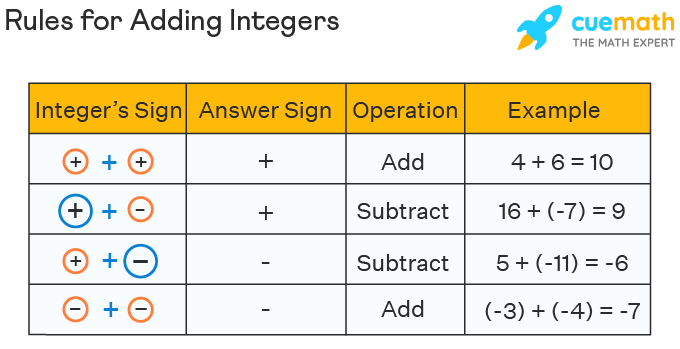
Adding Integers with the Same Sign
When we add two integers with the same sign, we add their absolute values and attach the common sign with the sum. For example, 2 + 3 = 5, (-2) + (-3) = - (2 + 3) = -5. The absolute value of a number is the positive value of the given number. For instance, the absolute value of 6 is 6, the absolute value of -6 is 6, and so on. Some examples of adding integers with the same sign are given below:
- (-1) + (-9) = - (1 + 9) = -10
- 3 + 8 = 11
- (-2) + (-17) = - (2 + 17) = -19
Use Cuemath's online adding integers calculator to verify these answers.
Adding Integers with Different Signs
Adding two integers with different signs is done by subtracting the absolute values, and then attaching the sign of the number with the greater absolute value. For example, if we want to add -2 and 3, first we find the absolute values of both. The absolute value of -2 is 2, and of 3 is 3. Now, find the difference between these absolute values which is 3 - 2 = 1. Since 3 > 2, and 3 has a positive sign, the sign of the resultant number will be positive. Therefore, - 2 + 3 = 1.
Adding Integers on a Number Line
The addition of integers on a number line is based on the given principles:
- Adding a positive number is done by moving towards the right side (or the positive side) of the number line.
- Adding a negative integer is done by moving towards the left side (or the negative side) of the number line.
- Any one of the given integers is taken as the base point from where we start moving on the number line.
Now, let us learn how to add integers on a number line.
- Step 1: The first step is to choose a scale on the number line. For example, whether we want to plot numbers in multiples of 1, 5, 10, 50, and so on depends on the given integers. For example, if we have to add 10 and -30, we can take a scale of 10 on the number line to ease our work.
- Step 2: If we have to add -2 and 7, we can take a scale of counting numbers starting from 1.
- Step 3: The next step is to locate any one of the integers on the number line, preferably a number with a greater absolute value. For example, if we need to add 2 and 19, it is better if we locate 19 on the line first and then take 2 jumps towards the right, rather than locating 2 and then take 19 jumps.
- Step 4: The final step is to add the second integer to the number located in the previous step by taking jumps either to the left or to the right depending on whether the number is positive or negative.
Let us take an example to understand more about adding integers on a number line.
Example: Use the number line and add the following integers: 5 + (-10)
Solution: Since we need to add a negative number (-10), we will move towards the left on the number line. Starting from 5, we will take 10 steps towards the left which will bring us to -5.

☛ Related Topics
Addition of Integers Examples
-
Example 1: Add the following integers by using the rules of integers in addition.
4 + (-6) + 13
Solution: There are three integers given. So, first let us add both the positive integers 4 and 13, which gives us 17. Now, we are left with the following expression 17 + (-6). Here, we have to apply the rule of addition of a negative and a positive integer. We get, 17 + (-6) = 11. Therefore, 11 is the result of the given integers.
-
Example 2: Using the rules of integers in addition, find which number should be subtracted from 13 to get -10 as the answer.
Solution: Let x be the number that needs to be subtracted from 13 to get -10. So, we can form an equation in terms of x.
13 - x = -10
- x = - 10 - 13
- x = -23
x = 23
Therefore, 23 needs to be subtracted from 13 to get -10.
-
Example 3: Add the following integers: -2 and -9.
Solution: While adding integers with the same sign, we add their absolute values and attach the common sign of the addends with the answer.
-2 + (-9) = - (2 + 9) = -11
Therefore, the sum of -2 and -9 is -11.

FAQs on Adding Integers
What is Addition of Integers?
Addition of integers means when we find the sum of integers. Since integers include positive numbers, negative numbers and zero, adding these may result in an increase or a decrease in value. This depends on whether the integers are positive or negative. For example, 5 + 6 = 11, and 5 + (-6) = -1, and -5 + 0 = -5
What are the Rules for Addition of Integers?
The rules for the addition of integers are listed below:
- The sum of an integer and its additive inverse is 0. For example, 6 + (-6) = 0
- Adding two positive integers always results in a positive value. For example, 6 + 6 = 12
- Adding two negative integers always results in a negative number. For example, -6 + (-6) = -12
- Adding a positive number with a negative number is done by finding the difference between the absolute value of both numbers. Then, the sign with the greater number gets attached to the sum. For example, +6 - 2 = +4
- Adding integers with 0 results in the same number. For example, 6 + 0 = 6, or -6 + 0 = -6
What is the Rule for Adding Integers with Different Signs?
For adding integers with different signs, we follow the steps given below. Let us add 5 and (-8)
- Step 1: Find the absolute values of the given integers. This means it will be 5 and 8.
- Step 2: Find the difference between the absolute values found in step 1. The difference of 5 and 8 is 3.
- Step 3: Attach the sign of the number with the greater absolute value. Since 8 has a negative sign, the answer will also have a negative sign. This means 5 + (-8) = -3
What is the Rule for Adding Integers with the Same Sign?
To add integers with the same sign, we add the absolute values of the numbers and then attach the common sign with the final answer. For example, (-9) + (-3) = -12.
How is Subtracting Integers Related to Adding Integers?
Subtracting integers is related to adding integers because when we add two integers with different signs, we find their absolute values and then find their difference, This means we make use of subtraction while we add integers with different signs. Apart from this, addition and subtraction are inverse operations. This means every addition expression can be expressed in subtraction and vice-versa. Subtracting integers is related to adding integers because both can be expressed in each other's form. For example, we can write 2 + (-9) as 2 - 9. Similarly, we can write - 3 - 5 as -3 + (-5).
What are the Steps for Adding Integers?
The steps for adding integers are given below:
- Find the absolute values of the given numbers.
- If both the numbers are of the same sign, then add the values. Attach the common sign with the answer.
- If they have different signs, then subtract them and find the difference between the absolute values. Then, the sign of the integer with the greater absolute value will attach to the final answer.
What is an Example of Adding Integers?
Some examples of the addition of integers are listed below:
- 3 + 8 = 11
- (-9) + (-4) = -13
- -6 + 4 = -2
- 12 + (-8) = 4
What is the Identity Element for Addition of Integers?
The identity element for addition of integers is zero (0). This is because when 0 is added to any integer, it results in the number itself. For example, 0 + 56 = 56, or, 0 + (-7) = -7
What are the Rules for Integers in Addition?
The rules for adding integers are given below:
- We first need to find the absolute value of the given integers.
- If both the numbers are of the same sign, then we add the values and attach the common sign with the answer.
- If they have different signs, then we subtract them and find the difference between the absolute values. Then, the sign of the integer with the greater absolute value will attach to the final answer.
- Adding integers with 0 results in the same number.
- The sum of an integer and its additive inverse is 0. For example, 4 + (-4) = 0
How to Add Positive and Negative Numbers?
In order to add positive and negative numbers, we need to use the following steps. Let us understand this with an example and add 7 + (-2)
- First, we need to find the absolute value of the given numbers. In this case, the absolute value of 7 is 7 and the absolute value of -2 is 2.
- Then, we find the difference between the absolute values. Here, it will be 7 - 2 = 5.
- Then, the sign of the integer with the greater absolute value will attach to the final answer. In this case, since 7 > 2, and 7 has a positive sign, the sign of the resultant number will be positive. Therefore, 7 + (-2) = 5.
How to Add Two Negative Numbers?
In order to add two negative numbers, we apply the rule which says that if the given numbers are of the same sign, then we add the values and attach the common sign with the answer. For example, let us add -7 + (-8). So, we will add the absolute values which is 7 + 8 = 15. Then, we will attach the common sign which is (-). Therefore, -7 + (-8) = -15.
visual curriculum