Inverse Sine
Inverse sine is one of the inverse trigonometric functions and it is written as sin-1x and is read as "sin inverse x". It is also written as arcsin (x) (read as 'arc sine x'). Please note that sin-1x (sin inverse x) is not the same as (sin x)-1 (reciprocal of sin x which is csc x). We have 6 inverse trigonometric functions such as:
- arcsin x = sin-1x = inverse of sin x
- arccos x = cos-1x = inverse of cos x
- arctan x = tan-1x = inverse of tan x
- arccsc x = csc-1x = inverse of csc x
- arcsec x = sec-1x = inverse of sec x
- arccot x = cot-1x = inverse of cot x
Here, we will study in detail about the inverse sine function (sin inverse) along with its graph, domain, range, and properties. Also, we will learn the formulas, derivatives, and integral of sin inverse x along with a few solved examples for a better understanding of the concept.
What is Inverse Sine?
The inverse sine function is the inverse of the sine function and thus it is one of the inverse trigonometric functions. It is also known as arcsin function which is pronounced as "arc sin". It is mathematically written as "asin x" (or) "sin-1x" or "arcsin x". We read "sin-1x" as "sin inverse of x". We know that if two functions f and f-1 are inverses of each other, then f(x) = y ⇒ x = f-1(y). So sin x = y ⇒ x = sin-1(y). i.e., when "sin" moves from one side to the other side of the equation, it becomes sin-1. Let us consider a few examples to see how the inverse sine function works.
Inverse Sine Examples
- sin 0 = 0 ⇒ 0 = sin-1(0)
- sin π/2 = 1 ⇒ π/2 = sin-1(1)
- sin π/6 = 0.5 ⇒ π/6 = sin-1(0.5)
Sin Inverse x Formula
In a right-angled triangle, the sine of an angle (θ) is the ratio of its opposite side to the hypotenuse. i.e., sin θ = (opposite side) / (hypotenuse). Then by the definition of inverse sine, θ = sin-1[ (opposite side) / (hypotenuse) ] . As the image below shows, to find the measure of the angle θ, we use the sin inverse x formula given by, θ = arcsin[ (opposite side) / (hypotenuse) ]. Inverse sine gives the measure of the angle for the corresponding value of the sine function such that the angle lies in the range of the sin inverse (We will discuss the domain and range of inverse sine in the next section.).
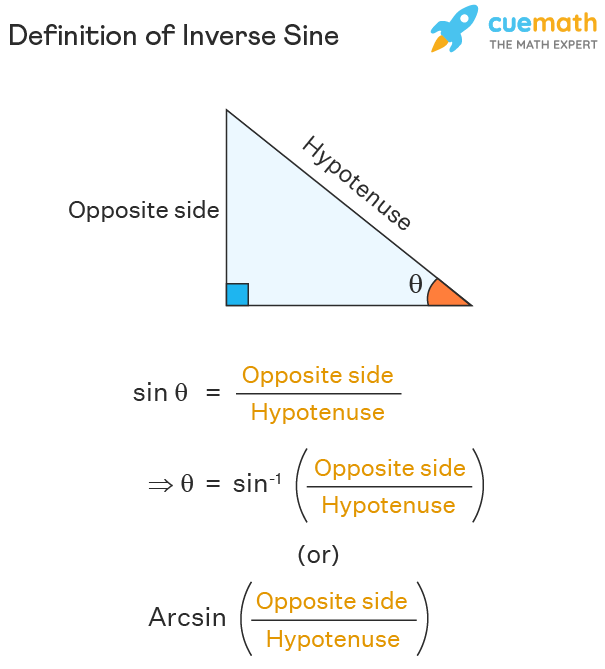
Thus, the inverse sine function is used to find the angle in a right-angled triangle when the opposite side and the hypotenuse are given. Also, it can be used to find the unknown angles in any triangle by using the sine law. In a triangle ABC, if AB = c, BC = a, and CA = b, then by the law of sines,
(sin A) / a = (sin B) / b
From this,
sin A = (a sin B) / b
A = sin-1 [ (a sin B) / b ]
Likewise, we can find the other angles of the triangle.
Domain and Range of Inverse Sine
In this section, let us see how can we find the domain and range of the inverse sine function. We know that the sine function is a function from R → [-1, 1]. But sine function is NOT one-one on the domain R and hence its inverse does not exist. For the sine function to be one-one, its domain can be restricted to one of the intervals [-3π/2, -π/2], [-π/2, π/2], [π/2, 3π/2], etc. Corresponding to each of these intervals, we get a branch of the inverse sine. But the domain of sine function is usually restricted to [-π/2, π/2] to make it one-one. The branch of sin inverse when the domain of sine function is [-π/2, π/2] is called the principal value branch.
We know that the inverse of a function exists if and only if it is bijective and the domain and range of a function are interchanged to be the range and domain of its inverse function respectively. Hence,
- the domain of sin inverse x is [-1, 1]
- the range of sin inverse x is [-π/2, π/2].
i.e., arcsin x (or) sin-1x : [-1, 1] → [-π/2, π/2]
Sin Inverse Graph
The graph of the inverse sine function with its range to be principal branch [-π/2, π/2] can be drawn using the following table. Here, we have chosen random values for x in the domain of sin inverse x which is [-1, 1]. We know the values of the sine function using the trigonometric table and using the functioning of the sin inverse function, we have the following table.
| x | y = sin-1x |
|---|---|
| -1 | sin-1(-1) = -sin-1(1) = -π/2 |
| -0.5 | sin-1(-0.5) = -sin-1(0.5) = -π/6 |
| 0 | sin-1(0) = 0 |
| 0.5 | sin-1(0.5) = π/6 |
| 1 | sin-1(1) = π/2 |
By plotting these points on the graph, we get the sin inverse graph.

Steps to Find Sin Inverse x
Here are the steps to find the sin inverse of x.
- Since the range of sin inverse x is [-π/2, π/2], the answer should lie in this interval.
- Assume that y = sin-1x. Then by the definition of inverse sine, sin y = x.
- Think what value of y in the interval [-π/2, π/2] satisfies the equation sin y = x and that is the answer.
Here are some examples to understand these steps.
Examples of Finding Sin Inverse of x
Note that sin-1x should always result in some angle that lies in the interval [-π/2, π/2].
- sin-1(1) = π/2 as sin π/2 = 1
- sin-1(-1) = -π/2 as sin (-π/2) = -1
- sin-1(-0.5) = -π/6 as sin (-π/6) = -0.5
Properties of Inverse Sine Function
Here are some properties/formulas of inverse sine. These are very helpful in solving the problems related to sin inverse in trigonometry.
- sin(sin-1x) = x only when x ∈ [-1, 1]
([When x ∉ [-1, 1], sin(sin-1x) is NOT defined) - sin-1(sin x) = x, only when x ∈ [-π/2, π/2]. To know how to calculate sin-1(sin x) when x ∉ [-π/2, π/2], click here.
- sin-1(-x) = -sin-1x, when x ∈ [-1, 1]
- sin-1(1/x) = csc-1x, when |x| ≥ 1
- sin-1x + cos-1x = π/2, when x ∈ [-1, 1]
- sin-1(2x √1 - x²) = 2 sin-1x, when -1/√2 ≤ x ≤ 1/√2 and
sin-1(2x √1 - x²) = 2 cos-1x, when 1/√2 ≤ x ≤ 1
Derivative of Inverse Sine
Let us find the derivative of y = sin-1x. By the definition of inverse sine, y = sin-1x can be written as sin y = x. Differentiating this on both sides with respect to x using the chain rule,
cos y (dy/dx) = 1
dy/dx = 1/cos y ... (1)
Now, we have sin2y + cos2y = 1 ⇒ cos2y = 1 - sin2y ⇒ cos y = √1 - sin²y = √1 - x²
Substituting this in (1),
dy/dx = 1/√1 - x²
Thus, the inverse sine derivative (or) the derivative of sin inverse x is 1/√1 - x².
Integral of Inverse Sine
We will find ∫ sin-1x dx using the integration by parts. For this, we write the above integral as
∫ sin-1x · 1 dx
Using LIATE, f(x) = sin-1x and g(x) = 1.
By integration by parts,
∫f(x) . g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) ∫g(x) dx) dx + C
∫ sin-1x · 1 dx = sin-1x ∫1 dx - ∫ [d/dx(sin-1x) ∫x dx] + C
∫ sin-1x dx = sin-1x (x) - ∫ [1/√1 - x²] x dx + C
Let us evaluate the integral on the right side using u-substitution method. For this, assume that 1 - x2 = u. From this, -2x dx = du (or) x dx = -1/2 du.
∫ sin-1x dx = x sin-1x - ∫(1/√u) (-1/2) du + C
= x sin-1x + 1/2 ∫u-1/2 du + C
= x sin-1x + (1/2) (u1/2/(1/2)) + C
= x sin-1x + √u + C
= x sin-1x + √(1 - x²) + C
Therefore, ∫ sin-1x dx = x sin-1x + √1 - x² + C.
Important Notes on Sin Inverse:
- Inverse sine can be written as sin-1 (or) arcsin (or) asin and it is a function with domain [-1, 1] and range [-π/2, π/2].
- Inverse sin is NOT same as (sin x)-1 as (sin x)-1 = 1/(sin x) = csc x.
- sin(sin-1x) is NOT always x. sin(sin-1x) = x only when x ∈ [-1, 1].
- sin-1(sin x) is NOT always x. sin-1(sin x) = x only when x ∈ [-π/2, π/2].
☛ Related Topics:
Inverse Sine Examples
-
Example 1: If θ is an acute angle in a right triangle whose opposite side is 4 units and the hypotenuse is 5 units, find θ.
Solution:
We know that sin θ = (opposite side) / (hypotenuse) = 4/5.
From the sin inverse x formula,
θ = sin-1 (4/5) ≈ 53.13 radians
(This is by using the calculator.)
Answer: θ ≈ 53.13 radians
-
Example 2: Find the values of the following: a) sin (sin-1 2) b) sin-1(sin 7π/6).
Solution:
a) We know that sin(sin-1 x) is NOT defined when x is NOT in [-1, 1] as the domain of inverse sine is [-1, 1].
Thus, sin(sin-1 2) is NOT defined.
b) sin-1(sin 7π/6)
Note that this is NOT equal to 7π/6 as 7π/6 ∉ [-π/2, π/2].
So we have to convert this angle to lie in the interval [-π/2, π/2].
We have sin 7π/6 = sin (π + π/6) = - sin π/6
Thus, sin-1(sin 7π/6) = sin-1(- sin (π/6))
We know that sin-1(-x) = - sin-1x. So
sin-1(sin 7π/6) = - sin-1(sin (π/6)) = -π/6 which lies in [-π/2, π/2]
Answer: a) sin(sin-1 2) is NOT defined b) sin-1(sin 7π/6) = -π/6.
-
Example 3: Prove the following: 3 sin-1x = sin-1(3x - 4x3), for x ∈ [-1/2, 1/2].
Solution:
Let us substitute x = sin θ in the RHS.
RHS = sin-1(3 sin θ - 4sin3θ)
From trigonometric formulas, we have
sin 3θ = 3 sin θ - sin3θ
So RHS = sin-1(sin 3θ)
= 3θ
= 3 sin-1x (because x = sin θ which implies θ = sin-1x using inverse sine definition)
= LHS
Answer: We have proved that 3 sin-1x = sin-1(3x - 4x3).

FAQs on Inverse Sine
What is Sin Inverse of x in Trigonometry?
Sin inverse of x is the inverse of the sine function. i.e., if y = sin x then x = sin-1(y). Here, sin-1 is the inverse function of sine.
How to Find the Inverse Sine of x?
To find the inverse sine of any number, just see what angle of sine gives that number. For example, sin-1(1/√2) = π/4 as sin π/4 = 1/√2. But make sure that the angle lies in the interval [-π/2, π/2] as the range of sin inverse is [-π/2, π/2].
What is the Sin Inverse of 1?
We know that sin π/2 = 1. Then by the definition of inverse sine, sin-1(1) = π/2. i.e., the value of inverse sine of 1 is π/2.
What is the Domain and Range of Sin Inverse?
We know that a function has an inverse if it is bijective but sine function is not one-one if its domain is R. So, we restrict its domain to [–π/2, π/2] to make it one-one and the range its is [–1, 1]. The domain and range of a function are interchanged to be the range and domain of its inverse function respectively. Hence,
- the domain of sin inverse x is [-1, 1]
- the range of sin inverse x is [-π/2, π/2].
Is the Inverse of Sine Csc?
No, the inverse of sine is not cosec. In fact, the inverse of sine is sin-1 (or) arcsin function. But note that (sin x)-1 = 1/(sin x) = csc x is the reciprocal of sine but this is not the inverse of the sine function.
How to Write Inverse Sine?
Inverse sine of x is written in one of the following ways:
- arcsin (x)
- asin (x)
- sin-1x
What is the Inverse Sine of 1/2?
We know that sin (π/6) = 1/2 and using the sin inverse x definition, we have sin-1(1/2) = π/6 which lies in the interval [-π/2, π/2].
Why do We Use the Inverse Sine Function?
The inverse sine function is used to find the angles in a right triangle when its opposite side and hypotenuse are known. i.e., angle = sin-1(opposite side to the angle/hypotenuse).
What is the Derivative of Sin Inverse x?
The derivative of sin-1x is 1/√1 - x². It is mathematically written as d/dx(sin-1x) = 1/√1 - x² (or) (sin-1x)' = 1/√1 - x².
What is the Integral of Inverse Sin?
The integral of sin-1x is x sin-1x + √1 - x² + C. It is mathematically written as ∫ sin-1x dx = x sin-1x + √1 - x² + C.
What is Inverse Sine of 2?
The domain of the inverse sine is [-1, 1]. Thus, it cannot take the value 2. So the inverse sine of 2 is not defined.
visual curriculum