Construction of Angles
The construction of angles is one of the most important aspects of geometry and is the "pure" form of geometric construction. The term construction in geometry refers to drawing shapes, lines, or angles accurately with the help of mathematical instruments. To construct angles, you will only need a pair of a compass or a protractor, a ruler (straightedge), and a pencil.
| 1. | Types of Angles |
| 2. | Construction of Angles Using a Protractor |
| 3. | Constructing Angles with Compass and Ruler |
| 4. | FAQs on Construction of Angles |
Types of Angles
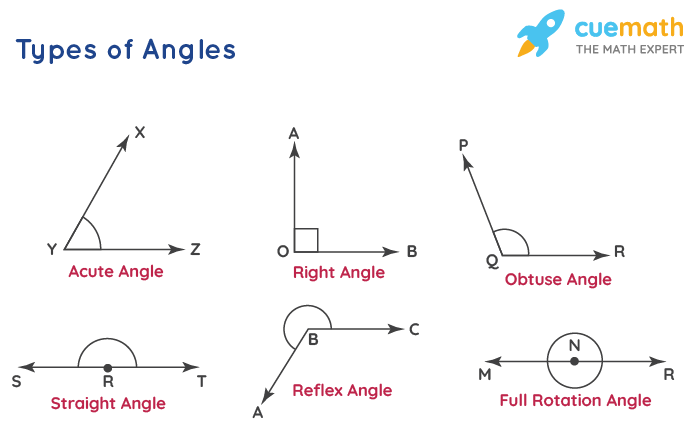
When two lines intersect and have a common endpoint that is when an angle is formed. Learning about angles in geometry is very important. Below are the 6 types of angles in geometry along with the degree measurement of angles.
- Acute Angle → An angle that measures less than 90°.
- Right Angle → An angle that measures exactly 90°.
- Straight Angle → An angle that measures equal to 180 degrees and looks like a straight line.
- Obtuse Angle → An angle that measures greater than 90° but less than 180°.
- Reflex Angle → An angle that always measures more than 180° (i.e. half a circle) but less than 360°.
- Full Rotation Angle → An angle that measures 360° exactly.
Constructing Angles Using a Protractor
An angle can be constructed either by using a protractor and a ruler or a compass and a ruler. Let us now look at the steps of constructing a 50° angle using a protractor.
- Step 1 - Draw a line segment OA.
- Step 2 - Place the center of the protractor at point O.
- Step 3 - Starting from point A in the clockwise direction and mark a point at 50 degrees by looking at the outer circle of the protractor. Label this point as B.
The ∠BOA is the required 50° angle.

Constructing Angles with Compass and Ruler
Let us learn how to construct an angle with a compass and a ruler. In the steps shown below we will be constructing an angle of 90° and then construct an angle bisector to bisect the 90° such that we will get an angle of 45°.
- Step 1: Draw a ray AB.
- Step 2: With A as the center and any width as radius draw a semicircular arc that touches the line segment AB and mark it as Q.
- Step 3: Without any change in radius, draw another arc with Q as the center and label this point as D.
- Step 4: Repeat the same process with D as the center and label the arc drawn as E.
- Step 5: Now, with the same radius and with E and D as centers draw arcs that intersect each other at a point and label it as F.
- Step 6: Now join the points A and F. This line is called the perpendicular line and it makes 90 degrees with the line segment AB.
- Step 7: Label the point of intersection of the semicircular arc with the line AF as P.
- Step 8: Now with the same radius taken to draw an arc in step 2, draw two arcs with P and Q as centers. Mark the point of intersection of these arcs as R. Now join the points A and R. Now ∠RAB and ∠FAR are equal to 45° each.

Topics Related to Construction of Angles
Check out some interesting articles related to the construction of angles.
Construction of Angles Examples
-
Example 1: Construct an angle of 75° using a compass and a ruler.
Solution:
Step 1: Draw a ray AB. With A as the center and any radius, draw an arc that cuts AB at C.
Step 2: With C as the center and the same radius, we draw an arc cutting the first arc at D, and with D as the center and the same radius, draw an arc that cuts the first arc at E
Step 3: With E and D as centers and with the same radius, we draw two arcs cutting each other at F. Join AF. The line AF makes 90° with the line segment AB.
Step 4: Mark the point where the line AF touches the semi-circular arc as G. Now with G and D as centers, draw two arcs again cutting each other at H. Now we join AH. ∠HAB= 75°.The construction of an angle of 75° is shown below.

-
Example 2: What are the steps to construct an angle of 105 degrees?
Solution:
Step 1: Draw a ray AB. With A as the center and any width as radius, draw an arc cutting AB at C.
Step 2: With C as the center and the same radius, we draw an arc cutting the first arc at D and, with D as the center and the same radius, draw another arc cutting again the first arc at G.
Step 3: With D and G as centers and with the same radius, we draw two arcs cutting each other at F. Join AF which is making 90°. Mark the point where the semicircular arc cuts the line AF as E.
Step 4: With G and E as centers and with the same radius draw two arcs cutting each other at H. Now join the points A and H.
∠HAB = 105°.


FAQs on Construction of Angles
What is Construction of Angles?
The construction of angles refers to constructing different angles such as 30°,45°, 60°,90° using a compass, protractor, ruler, and a pencil. This is considered to be the "pure" form of geometric constructions.
How to Construct a Right Angle?
A right angle is an angle whose measure is equal to 90 degrees. To construct a right angle, follow the steps given below:
- Draw a line segment AB and with A as the center and any radius, draw an arc such that it cuts AB at point C.
- Now, with C as the center and with the same radius as in the previous step, draw an arc intersecting the previously drawn arc at D.
- With D as the center and with the same radius, draw an arc such that it cuts the arc at E.
- With D and E as the centers and the same radius, draw two arcs intersecting at a point F. Join F and A. Now ∠FAB is a right angle that measures 90 degrees.
How to Construct an Angle with a Protractor?
Any angle between 0° and 180° can be easily constructed using a protractor. For example, we can construct an angle of 60° using a protractor by following the steps given below.
- We draw a line segment AB of any suitable length.
- Now, we place the protractor on the line segment AB.
- Then, we place the midpoint of the protractor at point A.
- On AB from the right, we start counting from 0° in the counter-clockwise direction and finally mark a point C showing 60° on the semi-circular edge of the protractor.
- We remove the protractor and join AC.
- We get the required angle ∠CAB = 60°.
How to Construct an Angle Bisector?
An angle bisector divides a given angle into two congruent angles. To construct an angle bisector, follow the steps given below:
- Draw a given angle using a protractor (say 60°). Let us name the vertices of the angle as A, B, and C such that angle ABC = 60 degrees.
- With B as the center and with more than half of BC as radius draw an arc on both the arms, which is AB and BC, and mark these points where the arc touches the line segments as D and E respectively.
- Now with D and E as the centers draw two arcs such that they intersect at a point. Label this point as F.
- Join F and B. FB is the angle bisector and now, ∠ABF and ∠FBC will measure 30 degrees each.
How do you Measure and Construct Angles?
An angle can be measured using a protractor which is a semi-circular disc used to draw and measure angles. Most protractors measure angles in degrees and are divided into 180 equal parts. They can be directly used to measure any angle within the range of 0° to 180° using the markings. We can use either protractor or a compass to construct angles of a specific measurement.
How are Angles Constructed?
To construct an angle with any degree of measure, we need to make use of a geometric tool called a compass. Once a ray is drawn, a compass is used to mark arcs according to any measured radius. These arcs intersect each other at various points which form perpendicular lines that make an angle. For more detailed steps, check out the construction of angle with compass and ruler section in this article.
How to Construct an Angle with a Compass?
An angle can be constructed by using two geometric tools, a compass and a ruler. Here are the steps to construct an angle with a compass:
- Draw any line segment AB.
- Keeping the pointed side of the compass on A, draw an arc intersecting the line segment at point S. The compass can be at any measurement.
- Keeping the same measurement, the pointed end is placed at point S and intersects the first arc at point R.
- Using a ruler, draw a line starting from point A joining the point R to form an angle.
- Use a protractor to measure the angle.
visual curriculum