L'Hopital's Rule
L'Hopital's rule (L'Hospital's rule) is pronounced as "lopeetals rule" and this rule is a very important rule in calculus that is used to evaluate weird limits that result in indeterminate forms (such as 0/0, ∞/∞, etc). These types of limits
- can't be calculated by direct substitution of the limit and/or
- can be evaluated but using a very long procedure.
Let us see the L'Hopital's Rule along with its statement, proof, and examples. Also, let us see some common misconceptions that may happen while the application of this rule.
L'Hopital's Rule History
L'Hopital's rule has various names such as L'Hospital's rule, L'Hôpital's rule, Bernoulli's rule, etc, and is used to evaluate the limits of indeterminate forms. It was first introduced by a Swiss mathematician Johann Bernoulli in 1694 and hence it is known as Bernoulli's rule. It was later developed by a French mathematician Guillaume de l'Hôpital and hence it became popular with the name L'Hopital's rule.
Let us examine an example before going to see what this rule says: lim x → 2 (x2 - 4) / (x - 2). The first thing we usually do to evaluate a limit is substituting the limit. Let us see what happens when we apply the limit. We get (22 - 4) / (2 - 2) = 0 / 0. This is an indeterminate form (as 0 / 0 is not defined). But let us try to simplify this limit in a different way. We know that x2 - 4 can be written as (x + 2) (x - 2) (using a² - b² formula). So lim x → 2 (x2 - 4) / (x - 2) = lim x → 2 [(x + 2) (x - 2)] / (x - 2) = lim x → 2 (x + 2) = 2 + 2 = 4. Because of the factorization, we could evaluate this limit easily.
Let us take another limit lim x → 0 (sin x) / x (whose actual value is 1 and this will be proved later) which also gives us an indeterminate form 0 / 0 but this cannot be evaluated easily as the other one. L'Hopital's Rule simplifies the process of finding limits that give indeterminate forms by the application of limit. Before going to learn it, let us just see what can be the other indeterminate forms.
Indeterminate Forms:
The indeterminate form is something that cannot be defined mathematically. Indeterminate forms can be of the form 0/0, ±∞/±∞, 0 × ∞, ∞ - ∞, 00, 1∞, ∞0, etc. But the most common indeterminate forms that encounter while the application of L'Hopital's rule are 0/0 and ±∞/±∞.
What is L Hospital Rule?
L'Hospital's rule states that the limit of the ratio of two functions (where the denominator is NOT equal to 0) that results in an indeterminate form by the direct application of the limit is equal to the limit of the ratio of their derivatives. Let us see the mathematical definition of L'Hopital's rule below.
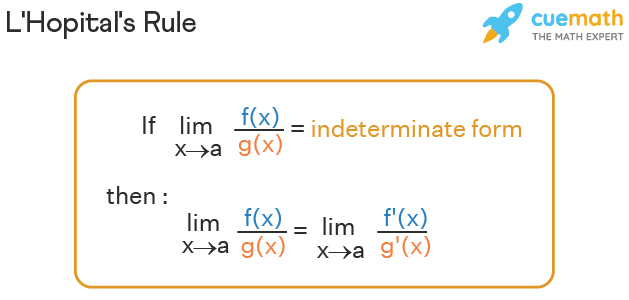
L'Hospital's Rule Formula
L'Hospital's rule states that for any two continuous functions f(x) and g(x), lim x → a f(x)/g(x) is an indeterminate form, then lim x → a f(x) / g(x) = lim x → a f' (x) / g'(x), where
- 'a' is any real number, or ∞, or - ∞.
- lim x → a f(x) / g(x) is an indeterminate form when x = a is applied.
- f'(x) is the derivative of f(x)
- g'(x) is the derivative of g(x) and g'(a) ≠ 0.
L'Hospital's Rule Proof
We know that L'Hopital's rule is applied when the limit is of the form 0/0 and ±∞/±∞. Let us assume that lim x → a f(x) / g(x) = 0 / 0. i.e., f(a) / g(a) = 0 / 0 which means f(a) = 0 and g(a) = 0. Let us consider the left hand side of the rule and we will ahchieve at the right hand side finally.
LHS = lim x → a f(x) / g(x)
= lim x → a [ f(x) - f(a) ] / [ g(x) - g(a) ] (∵ f(a) = g(a) = 0)
Dividing numerator and denominator by (x - a),
= lim x → a \(\dfrac{\frac{f(x)-f(a)}{x-a}}{\frac{g(x)-g(a)}{x-a}}\)
= \(\frac{lim_{x → a} \frac{f(x)-f(a)}{x-a}}{ lim_{x → a}\frac{g(x)-g(a)}{x-a}}\)
By the definition of derivative,
= f'(a) / g'(a)
= lim x → a f' (x) / g'(x)
= RHS
Hence L'Hopital's rule is proved. This proof is further extended to the limits with other indeterminate forms such as ±∞/±∞ (this proof is hard and advanced though).
When and How to Apply L'Hopital's Rule?
L'Hopital's rule should be applied only when lim x → a f(x) / g(x) leads to an indeterminate form by the direct application of limit. In such cases, we just differentiate the numerator and denominator (using derivative formulas) separately and then apply the limit. Here are the same examples that were mentioned in the first section and are solved using L'Hopital's rule very easily.
- lim x → 2 (x2 - 4) / (x - 2) = 0/0 by the direct application of limit (x = 2).
Using L'Hopital's rule:
lim x → 2 (x2 - 4) / (x - 2) = lim x → 2 (2x) / (1) = 2(2) = 4
(this follows from power rule) - lim x → 0 (sin x) / x = 0 / 0 when x = 0 is applied.
Using L'Hospital's rule:
lim x → 0 (sin x) / x = lim x → 0 (cos x) / 1 = cos 0 = 1
(this follows from the derivative of sin x formula)
Sometimes, the limit still results in an indeterminate form even after the application of L'Hopital's rule for one time. In that case, we can apply the same rule again and again as required.
Applying L'Hopital's Rule Multiple Times:
We can apply L'Hopital's rule as many times as required. Each time we apply the rule, we compute the derivatives of numerator and denominator functions separately and then apply the limit. But before each application of this rule, just make sure that the current limit leads to an indeterminate form. Here is an example.
Example: Evaluate the limit lim x → 0 (1 - cos 2x) / x2.
Solution:
By the direct application of limit x → 0, we get (1 - cos 0) / 0 = (1 - 1) / 0 = 0 / 0, which is an indeterminate form. So we apply L'Hospital's rule. We know that the derivatives of 1 - cos 2x and x2 are 2 sin 2x and 2x respecrively. Then the above limit becomes:
lim x → 0 (2 sin 2x / 2x) = lim x → 0 (sin 2x / x)
Let us try to apply the limit now. Then we get (sin 0) / 0 = 0 / 0, which is again an indeterminate form. So we apply the L'Hospital's rule again. We know that the derivatives of sin 2x and x are 2 cos 2x and 1 respectively. Then the above limit becomes:
lim x → 0 (2 cos 2x / 1) = 2 cos 0 = 2(1) = 2.
Therefore, lim x → 0 (1 - cos 2x) / x2 = 2.
Misconceptions of L'Hospital's Rule
There are some cases, where we tend to apply L'Hospital's rule but it results in a wrong result. So we have to be careful while applying this rule. Let us see where we can go wrong while applying the rule.
When Can't We apply L'Hospital's Rule?
Application of L'Hopital's rule when the limit does NOT give an indeterminate form throws the wrong result. For example:
lim x → 2 (3x + 1) / (2x + 2) = (3(2) + 1) / (2(2) + 2) = 7/6 (correct answer)
The limit didn't result in an indeterminate form and so we can't apply the L'Hospital's rule. Let us see what we get if we apply. We know that the derivatives of 3x + 1 and 2x + 2 are 3 and 2 respectively. So the above limit after the application of rule becomes:
lim x → 2 (3/2) = 3/2 (incorrect answer)
☛ So do apply the limit first and make sure that an indeterminate form is resulted before applying the rule.
Simplify the Fraction Before Each Application:
When we apply L'Hospital's rule for multiple times, simplify the rational expression each time before applying the limit every time. Otherwise, we result in a wrong answer. Here is an example.
lim x → 1 (x3 - 1) / (x2 - 1)
= lim x → 1 (3x2/2x)
= lim x → 1 (3x / 2)
= 3(1)/2
= 3/2 (correct answer)
But what happens if we don't simplify the fraction (in the third step) and try to apply L'Hopital's rule again?
lim x → 1 (x3 - 1) / (x2 - 1)
= lim x → 1 (3x2/2x)
= lim x → 1 (6x / 2)
= lim x → 1 3x
= 3(1)
= 3 (incorrect answer)
☛ Thus, simplify everything into the lowest terms before the application of the rule.
Important Notes on L'Hospital's Rule:
- The limit of a fraction of two functions (that results in an indeterminate form) is equal to the limit of the fraction of their derivatives.
- Do not apply L'Hospital's rule if the limit is not resulting in an indeterminate form.
- We can apply L'Hopital's rule as many times as required but before the application of each time, we should check whether the limit in that particular step is giving indeterminate form.
- When we are trying to apply L'Hopital's rule for the product f(x) · g(x), first, write it as fraction (i.e., either as f(x) / (1 / g(x)) or as g(x) / (1/ f(x)) ).
☛ Related Topics:
L'Hopital's Rule Examples
-
Example 1: Evaluate the limit lim x → ∞ (2x2 + 5x + 3) / (3x2 - 7x + 2) (i) without using and (ii) using L'Hopital's rule.
Solution:
(i) without using lHopitals rule:
lim x → ∞ (2x2 + 5x + 3) / (3x2 - 7x + 2)
= lim x → ∞ [x2 (2 + 5/x + 3/x2)] / [x2 (3 - 7/x + 2/x2)]
= lim x → ∞ (2 + 5/x + 3/x2) / (3 - 7/x + 2/x2)
= (2 + 0 + 0) / (3 - 0 + 0)
= 2/3(ii) using lHospitals rule:
lim x → ∞ (2x2 + 5x + 3) / (3x2 - 7x + 2)
Apply x → ∞ gives indeterminate form ∞/∞. So we apply L'Hospital's rule. The derivatives of numerator and denominator are 4x + 5 and 6x - 7 respectively. So the above limit becomes:
= lim x → ∞ (4x + 5) / (6x - 7)
Direct application of x → ∞ again gives ∞/∞. So we again apply the rule. Then we get:
= lim x → ∞ (4) / (6)
= 4/6
= 2/3Answer: In both the methods, we found that lim x → ∞ (2x2 + 5x + 3) / (3x2 - 7x + 2) = 2/3.
-
Example 2: Evaluate the limit lim x → ∞ (ex/x2).
Solution:
If we apply the limit x → ∞, it gives ∞/∞. So we apply L'Hpoital's rule. Then we get:
lim x → ∞ (ex/x2) = lim x → ∞ (ex/2x)
(This is by using the derivative of e^x formula)
Again, the application of limit gives ∞/∞. So we apply the rule again. Then the above limit becomes:
lim x → ∞ (ex/2) = ∞/2 = ∞
Answer: lim x → ∞ (ex/x2) = ∞.
-
Example 3: lim x → 0₊ (csc x - cot x).
Solution:
If we apply the limit we get the indeterminate form ∞ - ∞. So we first rewrite the expression using trig formulas and then apply L'Hospital's rule.
csc x - cot x = (1/sin x) - (cos x/ sin x) = (1 - cos x) / (sin x).
Then the above limit becomes:
lim x → 0₊ (csc x - cot x)
= lim x → 0₊ [(1 - cos x) / (sin x)]The derivatives of numerator and denominator are sin x and cos x respectively. Then the above limit by applying the rule again becomes:
= lim x → 0₊ (sin x) / (cos x)
= (sin 0)/(cos 0)
= 0/1
= 0Answer: lim x → 0₊ (csc x - cot x) = 0.

FAQs on L'Hopital's Rule
What is L'Hopital's Rule in Calculus?
L'Hopital's rule in Calculus works very well in evaluating limits whose value is an indeterminate value after the direct application of limit. To apply this rule, we just replace the given fraction of functions with the fraction of their derivatives and then apply the limit. We can always apply this rule as many times as needed.
How to Apply L'Hospital's Rule?
To apply L'Hopital's rule to evaluate a limit lim x → a f(x)/g(x):
- First check whether f(a)/g(a) results in an indeterminate form such as 0/0, ∞/∞, etc.
- If so, find the derivatives f'(x) and g'(x).
- Then the given limit is obtained by evaluating the limit lim x → a f'(x)/g'(x).
What is L Hospital Rule Formula?
The formula of L Hopitals rule is lim x → a f(x) / g(x) = lim x → a f' (x) / g'(x), where the left side limit gives an indeterminate form by applying the limit x = a. Here f'(x) and g'(x) are the derivatives of the respective functions.
How Do You Know if L'Hospital's Rule Apply?
To evaluate any limit as x → a, we first substitute x = a in the given expression. If this results in an indeterminate value such as 0/0, ∞/∞, ∞/0, etc, then we apply L'Hopital's rule.
When Can't You Use L'Hopital's Rule?
When the application of the limit to a fraction of functions results in any real number, or ∞, or -∞, then we shouldn't apply L'Hopital's rule to that limit.
Can We Use L'Hopital's Rule Multiple Times?
Yes, we can use L'Hopital's rule multiple times. But make sure before each application of the rule that the application of the limit is resulting an indeterminate value like 0/0.
How do You Pronounce L'Hospital's Rule?
L'Hospital's rule is actually called L'Hopital's rule (which was derived by a French mathematician Guillaume de l'Hôpital) and it is pronounced as "lopeetals rule". It is used to evaluate the limits that are resulting in indeterminant form.
How do You Apply L'Hopital's Rule for Exponents?
While finding the limits, if a variable is present in the expression, first label the limit as L and then apply the logarithm on both sides. For example, to evaluate the limit lim x → ∞ x1/x, first assume that L = lim x → ∞ x1/x. Then taking "ln" on both sides,
ln L = lim x → ∞ ln x1/x
ln L = lim x → ∞ (1/x) ln x
ln L = lim x → ∞(ln x) / x
By L'Hospital's rule,
ln L = lim x → ∞ (1/x) / 1
ln L = 0
L = e0 = 1
Therefore, lim x → ∞ x1/x = 1.
visual curriculum