Types of Fractions
Before exploring the types of fractions, let us recall fractions. A fraction is a portion or part of any quantity out of a whole, where the whole can be any number, a specific value, or a thing. In many real-time situations, each and every quantity to be measured cannot be an absolute whole number. Hence, we may have to deal with parts of a whole or portions of a whole. This is where the concept of fractions comes in. In this lesson, let us learn about different types of fractions with examples, such as proper and improper fractions, mixed fractions, equivalent fractions, like and unlike fractions.
| 1. | What are the Different Types of Fractions? |
| 2. | Improper Fraction to Mixed Fraction |
| 3. | Mixed Fraction to Improper Fraction |
| 4. | FAQs on Types of Fractions |
What are the Different Types of Fractions?
The different types of fractions are distinguished mostly on the basis of their numerator and denominator. A fraction consists of two parts, the numerator, and the denominator. The numerator is the number that is placed on the top of the fractional bar, while the number that is placed on the bottom is called the denominator. The numerator indicates the number of parts that are being considered, whereas, the denominator indicates the total number of parts in the whole.
Although there are many types of fractions, the three main types of fractions that are differentiated on the basis of the numerator and the denominator are:
- Proper fractions
- Improper fractions
- Mixed fractions
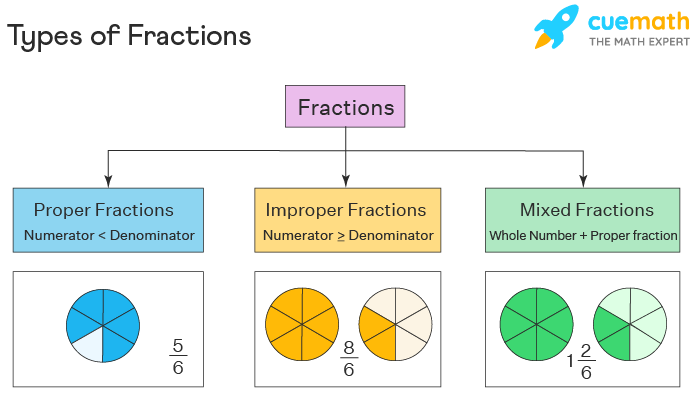
Proper Fractions
A fraction whose numerator is less than its denominator is called a proper fraction. For example, 3/12 and 2/5 are proper fractions because 3 < 12 and 2 < 5. Example: Sam got a bar of chocolate and he divided it into 3 equal parts. He took 1 part and gave 2 parts to his sister, Sara. We can represent Sam's portion as 1/3 and Sara's portion as 2/3. Both these fractions are considered proper fractions.
Improper Fractions
A fraction whose numerator is greater than or equal to its denominator is called an improper fraction. For example, 5/2 and 8/7 are improper fractions because 5 > 2 and 8 > 7.
Mixed Fractions
A mixed fraction is a mix of a whole number and a proper fraction. For example, \(1 \dfrac{3}{4}\) and \(3 \dfrac{4}{7}\) are mixed numbers or mixed fractions. In the first example, 1 is the whole number part and 3/4 is the proper fraction. In the second example, 3 is the whole number part and 4/7 is the proper fraction.
Now, let us study the types of fractions that are classified in groups. When a group of fractions is classified they help in comparing fractions. They are categorized as follows:
- Like fractions
- Unlike fractions
- Equivalent fractions
Like Fractions
If the denominators of two or more fractions are the same, then they are called like fractions. For example 1/6, 2/6, 3/6, 5/6, are known as like fractions. We can perform addition and subtraction of fractions only on like fractions. In some cases, we need to convert unlike fractions to like fractions to add or subtract.
Unlike Fractions
If the denominators of two or more fractions are different, then the fractions are termed as unlike fractions. For example 1/2, 1/3, 2/5, 3/6, etc. If the fractions are unlike, while adding or subtracting the fractions, we convert them to like fractions.
Equivalent Fractions
Equivalent fractions are the fractions that have different numerators and different denominators but are equal to the same value when simplified or reduced. For example, 2/4, 3/6, 4/8 are all equivalent fractions because they all get reduced to 1/2.
Apart from these, there are fractions with 1 as the numerator. Let us read about them.
Unit Fractions
Units fractions are those fractions in which the numerator is 1 and the denominator is a positive integer. For example, 1/3, 1/8, 1/19, 1/23, and so on are called unit fractions.
Improper Fraction to Mixed Fraction
To convert improper fractions to mixed fractions, we need to divide the numerator by the denominator. Then, we write it in the mixed number form by placing the quotient as the whole number, the remainder as the numerator and the divisor as the denominator. Let us go through the following example to understand this better. Let the improper fraction be 12/5. To convert it into a mixed fraction, we follow these steps:
- Step 1: Divide 12 by 5.
- Step 2: On dividing, we obtain the quotient as 2 and the remainder as 2.
- Step 3: The quotient becomes the whole number part and the remainder 2 becomes the new numerator, while the denominator remains the same.
- Step 4: Thus, the improper fraction, 12/5 is written as a mixed fraction and is represented as \(2\dfrac{2}{5}\)
Mixed Fraction to Improper Fraction
A mixed fraction is a mixture of a whole number and a proper fraction. In order to convert a mixed fraction to an improper fraction, we need to multiply the denominator with the whole number part and then add the numerator to the product. The resultant will be the new numerator, whereas, the denominator remains the same. Let us go through the following example to understand this better. Let the mixed fraction be \(7\dfrac{3}{5}\). To convert this into an improper fraction, we follow these steps:
- Step 1: Multiply the whole number 7 with the denominator 5. So, we get 7 × 5 = 35
- Step 2: Add the product with the numerator: 35 + 3 = 38
- Step 3: Express it as a fraction with the denominator 5, that is, 38/5
Tips on Types of Fractions
Given below are a few important points related to the different types of fractions:
- The value of an improper fraction is always greater than 1.
- The value of a proper fraction is always less than 1.
- A mixed fraction is the combination of a whole number and a fraction.
- A mixed fraction can be converted into an improper fraction and vice versa. For example, \(2\dfrac{1}{2}\) = 5/2.
☛ Related Topics
FAQs on Types of Fractions
How many Types of Fractions are there?
There are 7 different types of fractions that are classified according to various categories.
- When fractions are classified on the basis of the numerator and the denominator, they are categorized as proper fractions, improper fractions, mixed fractions.
- When they are classified in groups they are categorized as like fractions, unlike fractions and equivalent fractions.
- Then, there are units fractions which have 1 as the numerator.
What are the Three Types of Fractions?
The three types of fractions, based on the numerator and the denominator are proper, improper, and mixed fractions. For example, 2/5, 3/4 are termed as proper fractions because here the numerator is smaller than the denominator; 5/2, 8/3 are termed as improper fractions because the numerator is greater than the denominator; and \(1\dfrac{2}{6}\) and \(3\dfrac{1}{4}\) are termed as mixed fractions because they consist of a whole number and a proper fraction.
How to Solve all Types of Fractions?
Fractions can be solved according to the category to which they belong. The different types of fractions are solved using the following ways.
- To add and subtract like fractions, we just solve the numerators while the denominators remain the same. For example, 1/3 + 4/3 = 5/3, 9/4 - 3/4 = 6/4
- For unlike fractions, they are first converted into like fractions in order to add or subtract them. For example, to add 1/3 + 1/2, we need to find the Least Common Multiple (LCM) of the denominators and convert the given fractions to like fractions that are equivalent to them. Here, they are converted and written as 2/6 + 3/6, and then we add them which results in (2 + 3)/6 = 5/6
- Multiplication of two given fractions is done by multiplying the numerators and then multiplying the denominators. After this, they are reduced to their lowest terms, if needed. For example, 1/3 × 1/2 = 1/6
- Division of fractions is done by multiplying the first fraction with the reciprocal of the second fraction. For example, 1/3 ÷ 1/2 = 1/3 × 2/1 = 2/3
What are Proper Fractions?
The fraction in which the numerator is less than the denominator is called a proper fraction. For example, 5/12 and 3/8 are proper fractions.
What are Two Parts of a Fraction?
A fraction has two parts, the numerator and the denominator.
- Numerator: The numerator represents the number that is placed on the top of the fraction. It represents the part that is considered out of the whole. For example, in 5/6, 5 is the numerator.
- Denominator: The denominator indicates the part that is placed on the bottom of the fraction. It represents the total number of parts. For example, in 5/6, 6 is the denominator.
What is a Mixed Fraction?
A fraction that is a combination of a whole number and a proper fraction is termed as a mixed fraction. For example, \(2\dfrac{1}{3}\) a mixed fraction, where 2 is the whole number part, and 1/2 is the proper fraction.
What are Similar Fractions?
Similar fractions are also known as like fractions. Two or more fractions having exactly the same denominator are termed as like fractions or similar fractions. In other words, the fractions with the same denominators are called like fractions. For example, 1/7, 2/7, 5/7, 6/7 are all like fractions, with the same denominator, that is, 7.
What are the 7 Types of Fractions with Examples?
The 7 types of fractions with examples are given as follows:
- Proper Fractions: Proper fractions are those fractions in which the numerator is smaller than the denominator. For example, 3/4, 7/19, 67/543, and so on.
- Improper Fractions: Improper fractions are those fractions in which the numerator is larger than the denominator. For example, 13/4, 57/9, 567/83, and so on.
- Mixed Fractions: Mixed fractions or Mixed numbers are those fractions that consist of a whole number part and a fractional part. For example, \(2 \dfrac{6}{7}\) and \(8 \dfrac{3}{4}\).
- Like Fractions: Like fractions are expressed as a group of fractions that have the same denominator. For example, 8/9, 5/9, 4/9 are like fractions because their denominators are the same.
- Unlike Fractions: Unlike fractions are expressed as a group of fractions that have different denominators. For example, 6/7, 5/8, 3/5 are unlike fractions because their denominators are different.
- Equivalent Fractions: Equivalent fractions are those fractions that have different numerators and different denominators but are equal to the same value when simplified or reduced. For example, 13/26, 14/28, 20/40 are equivalent fractions because they all get reduced to the same fraction, that is, 1/2.
- Unit Fractions: Unit fractions are those fractions in which the numerator is 1 and the denominator is a positive integer. For example, 1/2, 1/27, 1/56, and so on.
What Kind of Fractions have Different Denominators?
Fractions that have different denominators are called unlike fractions. These fractions are represented in groups. For example, 7/9, 2/5, 3/6 are unlike fractions because they have different denominators.