Geometry Formulas
Geometry formulas are used for finding dimensions, perimeter, area, surface area, volume, etc. of the geometric shapes. Geometry is a part of mathematics that deals with the relationships of points, lines, angles, surfaces, solids measurement, and properties. There are two types of geometry: 2D or plane geometry and 3D or solid geometry.
The 2D shapes are flat shapes that have only two dimensions, length, and width as in squares, circles, and triangles, etc. 3D objects are solid objects, that have three dimensions, length, width, and height or depth, as in a cube, cuboid, sphere, cylinder, cone. Let us learn all geometry formulas along with a few solved examples in the upcoming sections.
What are Geometry Formulas?
The formulas used for finding dimensions, perimeter, area, surface area, volume, etc. of 2D and 3D geometric shapes are known as geometry formulas. 2D shapes consist of flat shapes like squares, circles, and triangles, etc., and cube, cuboid, sphere, cylinder, cone, etc are some examples of 3D shapes. The basic geometry formulas are given as follows:
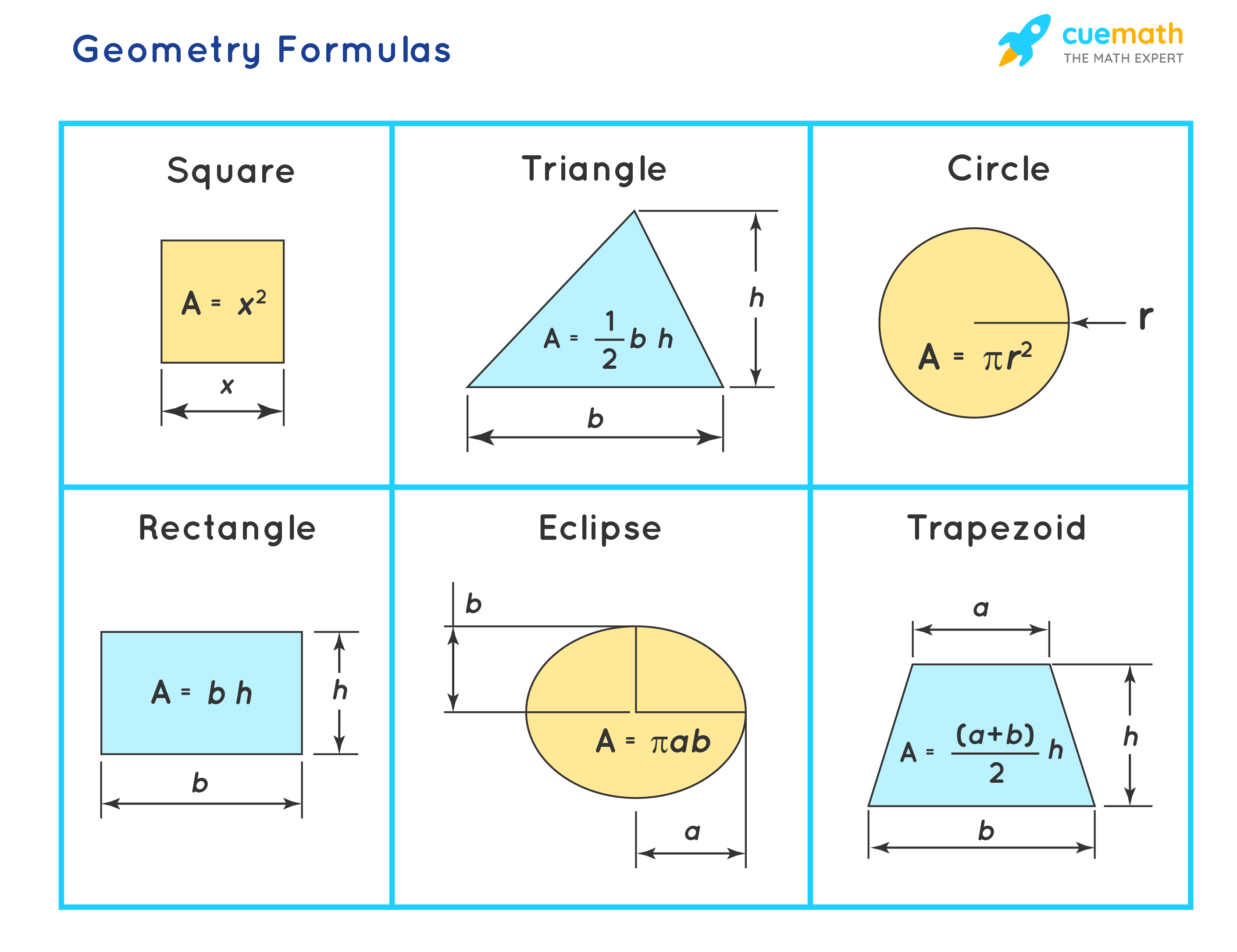
Basic Geometry Formulas
Let us see the list of all Basic Geometry Formulas here.
2D Geometry Formulas
Here is the list of various 2d geometry formulas according to the geometric shape. It also includes a few formulas where the mathematical constant π(pi) is used.
- Perimeter of a Square = 4(Side)
- Perimeter of a Rectangle = 2(Length + Breadth)
- Area of a Square = Side2
- Area of a Rectangle = Length × Breadth
- Area of a Triangle = ½ × base × height
- Area of a Trapezoid = ½ × (base1 + base2) × height
- Area of a Circle = A = π×r2
- Circumference of a Circle = 2πr
3D Geometry Formulas
The basic 3D geometry formulas are given as follows. It should be noted that the following formulas have used the mathematical constant π(pi)
- The curved surface area of a Cylinder = 2πrh
- Total surface area of a Cylinder = 2πr(r + h)
- Volume of a Cylinder = V = πr2h
- The curved surface area of a cone = πrl
- Total surface area of a cone = πr(r+l) = πr[r+√(h2+r2)]
- Volume of a Cone = V = ⅓×πr2h
- Surface Area of a Sphere = S = 4πr2
- Volume of a Sphere = V = 4/3×πr3
where,
- r = Radius;
- h = Height. and,
- l = Slant height
The formula table depicts the 2D geometry formulas and 3D geometry formulas.
| SHAPES | FORMULAS |
|---|---|
| 1. Right Triangle |
Pythagoras Theorem: base2 + height2 = hypotenuse2 Area = ½ × base × height Perimeter = base + height + hypotenuse |
| 2. Triangle |
Perimeter, P = a + b + c Where, a, b, and c are the sides of a triangle. Area, A = ½ base × height |
| 3. Rectangle |
Perimeter = 2(l + w) Area = lw Diagonal, d = √(l2 + w2) Where, l = length of a rectangle w = width of a rectangle |
| 4.Parallelogram |
Perimeter, P = 2(a + b) Where, a and b are the sides of a parallelogram Area of parallelogram, A = base × height Height, h = Area/base Base, b = Area/height |
| 5. Trapezium |
Area, A = ½(a + b)h Where, a and b are the parallel sides h = distance between two parallel sides |
| 6. Circle |
Circumference = 2πr Area = πr2 Diameter = 2r Where, r = radius of a circle |
| 7. Square |
Perimeter, P = 4a Area, A = a2 Diagonal, d = a√2 Side, a = √A Where, a = side of a square |
| 8. Arc |
Arc Length, L = rθ Here, θ is the central angle in radians and r = radius |
| 9. Cube |
Area, A = 6a2 Volume, V = a3 Edge, a = Volume⅓ Space diagonal = a√3 Where, a = side of a cube |
| 10. Cuboid |
Surface Area, A = 2(lb + bh + hl) Volume, V = lbh Space diagonal, d = √( l2 + b2 +h2) Where, l= length b= breadth h= height |
| 11. Cylinder |
Total Surface Area, A = 2πrh + 2πr2 Curved Surface Area, Ac = 2πrh Volume, V = πr2h Base Area, Ab = πr2 Radius, r = √(V/πh) Where, r= radius of a cylinder h= height of a cylinder |
| 12. Cone |
Total Surface Area, A = πr(r+l) = πr[r+√(h2+r2)] Curved Surface Area, Ac = πrl Volume, V = ⅓πr2h Slant Height, l = √(h2+r2) Base Area, Ab = πr2 Where, r= radius of a cone h= height of a cone l = slant height |
| 13. Sphere |
Surface Area, A = 4πr2 Volume, V = ⁴⁄₃πr3 Diameter = 2r Where, r= radius of a sphere |
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.

Let us have a look at solved examples to understand the basic geometry formulas.
Solved Examples Using Geometry Formulas
Example 1: Calculate the circumference and the area and of a circle by using geometry formulas if the radius of the circle is 21 units.
Solution:
To find the area and the circumference of the circle.
Given: Radius of a circle = 21 units
Using geometry formulas for circle,
Area of circle = π × r2
= 3.142857 × 212
= 1385.44
Now for the circumference of the circle,
Using geometry formulas for circle,
Circumference of a Circle = 2πr
= 2(3.142857)(21)
= 131.95
Answer: The area of a circle is 1385.44 square units and the circumference of a circle is 131.95 units.
Example 2: What is the area of a rectangular park whose length and breadth are 90 m and 60 m respectively?
Solution:
To find the area of a rectangular park:
Given: Length of the park = 90 m
The breadth of the park = 60 m
Using the geometry formulas for a rectangle,
Area of Rectangle = (Length × Breadth)
= (90 × 60) m2
= 5400 m2
Answer: The area of the rectangular park is 5400 m2.
Example 3: Using geometry formulas of the cube, calculate the surface area and volume of a cube whose edge is 6 units.
Solution:
To Find: The surface area and volume of a cube whose edge is 6 units
Using geometry formulas of cube,
Surface area of cube is = A = 6a2
A = 6 (6)2
A = 6 × 36 = 216 units2
Volume of a cube, V = a3
V = (6)3
V = 216 units3
Answer: The surface area of the cube is 216 units2. The volume of the cube is 216 units3
FAQs on Geometry Formulas
What are the Geometry Formulas of a Cuboid?
The geometry formulas of a cuboid are listed below:
- Surface Area of cuboid, A = 2(lb + bh + hl)
- Volume of cuboid, V = lbh
- Space diagonal of cuboid, d = √(l2 + b2 +h2)
Where,
- l= length
- b= breadth
- h= height
What are the Geometry Formulas of a Rectangle?
The geometry formulas of a rectangle are listed below:
- Perimeter of a rectangle = 2(l + w)
- Area of rectangle = lw
- Diagonal of a rectangle, d = √(l2 + w2)
Where,
- l = length of a rectangle
- w = width of a rectangle
What are the Geometry Formulas of a Cone?
The geometry formulas of a cone are listed below:
- Total surface area of cone, A = πr(r+l) = πr[r+√(h2+r2)]
- Curved surface area of cone, Ac = πrl
- Volume of cone, V = ⅓πr2h
- Slant Height of cone, l = √(h2+r2)
- Base Area, Ab = πr2
Where,
- r= radius of a cone
- h= height of a cone
- l = slant height
What are the Geometry Formulas of a Circle?
The geometry formulas of a circle are listed below:
- Circumference = 2πr
- Area = πr2
- Diameter = 2r
Where, r = radius of a circle
What are the Geometric Formulas of a Sphere?
The two important geometry formulas of a sphere are the area and volume of a sphere. The formula for the surface area of a sphere is A = 4πr2 and the formula for the volume of the sphere is V = ⁴⁄₃πr3.
What are the Applications of Geometry Formulas?
Geometry formulas are useful to find the perimeter, area, volume, and surface areas of two-dimensional and 3D Geometry figures. In our day-to-day life, there are numerous objects which resemble geometric figures and the areas and volumes of these geometric figures can be calculated using these geometric formulas.
How to Learn All Geometry Formulas?
All geometry formulas are given in detail above on this page for reference. These formulas can be learnt with practice when the students use them repeatedly. Another way to memorize the geometry formulas is that the students should make a chart of all these formulas and paste it on a place or wall where they usually study. This will help them glance through the formulas more often and this will passively be absorbed by them.
visual curriculum